Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T13:19:07.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Some renewal theorems for random walks in multidimensional time

Published online by Cambridge University Press:  24 October 2008

Makoto Maejima  and
Toshio Mori
Makoto Maejima
Affiliation:
Department of Mathematics, Keio University, Yokohama 223, Japan
Toshio Mori
Affiliation:
Department of Mathematics, Yokohama City University, Yokohama 236, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

Let Kr denote the set of r-tuples n = (n1n2, …, nr) with positive integers as coordinates (r ≥ 1) and {X, Xn, n ε Kr} be a family of independent, identically distributed random variables with positive mean 0 < EX ≡ μ < ∞ and finite positive variance 0 < var X ≡ σ2 ∞. The notation m ≤ n, where m = (mi) and n = (ni), means that mi ≤ ni (i = 1, 2,…, r) and |n| = n1n2 … nr. Denote Sn =Σj ≤ nXj (j, n ε Kr). When r = 1, {Xn, n ε Kr) reduces to the sequence {Xj, j ε 1} of independent random variables each distributed as X, and Sn becomes the ordinary partial sum .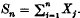

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 1 , January 1984 , pp. 149 - 154
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Chung, K. L. and Pollard, H.. An extension of renewal theory. Proc. Amer. Math. Soc. 3 (1952), 303–309.CrossRefGoogle Scholar
[2] Erdös, P., Feller, W. and Pollard, H.. A property of power series with positive coefficients. Bull. Amer. Math. Soc. 55 (1949), 201–204.CrossRefGoogle Scholar
[3] Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers (Oxford, 1960).Google Scholar
[4] Heath-Brown, D. R.. Mean values of the zeta function and divisor problems. Recent Progress in Analytic Number Theory, vol. 1 (ed. Halberstan, H. and Hooley, C.), (1981), 115–119.Google Scholar
[5] Katz, M. L.. The probability in the tail of a distribution. Ann. Math. Statist. 34 (1963), 312–318.CrossRefGoogle Scholar
[6] Ney, P. and Wainger, S.. The renewal theorem for a random walk in two-dimensional time. Studia Mathematica 46 (1972), 71–85.CrossRefGoogle Scholar
[7] Petrov, V. V.. Sums of Independent Random Variables (Springer, 1975).Google Scholar
[8] Smith, W. L.. Extension of a renewal theorem. Proc. Cambridge Philos. Soc. 51 (1955), 629–638.CrossRefGoogle Scholar
[9] Titchmarsh, E. C.. The Theory of the Riemann Zeta Function (Oxford, 1951).Google Scholar