Published online by Cambridge University Press: 24 October 2008
Let f(t) be defined and measurable for t > 0, and suppose that it has non-vanishing moment constants
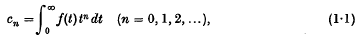
where the integrals are Cauchy-Lebesgue integrals, 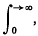 or possibly
or possibly 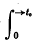 if f(t) is null for t > t0 but not for t < t0 (a convention to which we adhere throughout).
if f(t) is null for t > t0 but not for t < t0 (a convention to which we adhere throughout).
* See Bromwich(1), § 118.
* I.e. Mittag-Leffler's generalization of Borel's exponential method. Hardy calls g the (B, α) method. α = 1 is Borel's case.
* See a forthcoming research note to appear in the Proceedings.
* More precisely ‘the ![]() Mellin transforms.
Mellin transforms.
* See the end of § 1.
* ![]() When
When ![]() Incidentally, in this case ø is equal to the first term of its asymptotic expansion. The value of C in Hardy [(4), § 4] should be 1/√(4π). If we assume
Incidentally, in this case ø is equal to the first term of its asymptotic expansion. The value of C in Hardy [(4), § 4] should be 1/√(4π). If we assume ![]() the values of the constants can be found easily by equation (4·6) (using Stirling's formula). This method was used by Hardy (in rough notes) to obtain the result given in § 5 of Hardy(4). A further correction to this paper of Hardy's, as regards the series ∑(−)nn!, is to appear as a note in J. London Math. Soc.
the values of the constants can be found easily by equation (4·6) (using Stirling's formula). This method was used by Hardy (in rough notes) to obtain the result given in § 5 of Hardy(4). A further correction to this paper of Hardy's, as regards the series ∑(−)nn!, is to appear as a note in J. London Math. Soc.
* The integrand is analytic and single-valued in the shaded region if t α is taken as | t |αeiαθ where t = | t | e iθ, − 2π < θ < 0. We may suppose that the contour of ![]() nowhere meets the positive real axis.
nowhere meets the positive real axis.
* Namely ![]() where η and η′ are small (depending only on α).
where η and η′ are small (depending only on α).
† It is not necessary to know in advance that the values of B and λ are the same as before.
* τ in § 7 should not be confused with the τ of § 5.
* By ψ(ω) ε V(a, b) we mean that ψ(ω) is of bounded variation in (a, b).
† Actually the first term of (5·1) vanishes, but we avoid using this to give the best chance of eliminating the condition δ ≥ γ.
‡ Each A depends also on the choice of previous A's. The point here of course is that A is independent of τ.
* The O's and K′, which is positive, depend only on c, d, γ, ω 0, ω 1.
* I.e. for the purpose of proving (8·3) and (8·4).
* Or once less if (δ − γ)/c happens to be an integer.
* While on the subject of generalizations of results concerning Borel summation I would like to add that the ‘Borel-Tauber’ theorem of Hardy and Littlewood(5) can be generalized to a (B, α)-Tauber theorem; namely, that if a series is summable (B, α) and its terms are O(n −i) then it is convergent. No doubt there are Tauberian theorems for more general moment methods corresponding to the results for integral function methods due to Valiron(10).
* We have, however, changed α (= c/d) to μ, to prevent confusion with the α in the statement of the theorem of the present section.