Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T13:18:40.726Z Has data issue: false hasContentIssue false
  • English
  • Français

Some reductions of the spectral set conjecture to integers

Published online by Cambridge University Press:  25 September 2013

DORIN ERVIN DUTKAY  and
CHUN–KIT LAI
DORIN ERVIN DUTKAY
Affiliation:
University of Central Florida, Department of Mathematics, 4000 Central Florida Blvd., P.O. Box 161364, Orlando, FL 32816-1364, U.S.A. e-mail: [email protected]
CHUN–KIT LAI
Affiliation:
McMaster University, Department of Mathematics and Statistics, 1280 Main Street West, Hamilton, Ontario, CanadaL8S 4K1 e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

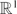The spectral set conjecture, also known as the Fuglede conjecture, asserts that every bounded spectral set is a tile and vice versa. While this conjecture remains open on ${\mathbb R}^1$, there are many results in the literature that discuss the relations among various forms of the Fuglede conjecture on 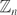${\mathbb Z}_n$, 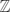${\mathbb Z}$ and 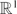${\mathbb R}^1$ and also the seemingly stronger universal tiling (spectrum) conjectures on the respective groups. In this paper, we clarify the equivalences between these statements in dimension one. In addition, we show that if the Fuglede conjecture on 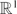${\mathbb R}^1$ is true, then every spectral set with rational measure must have a rational spectrum. We then investigate the Coven–Meyerowitz property for finite sets of integers, introduced in [1], and we show that if the spectral sets and the tiles in 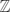${\mathbb Z}$ satisfy the Coven–Meyerowitz property, then both sides of the Fuglede conjecture on 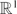${\mathbb R}^1$ are true.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 1 , January 2014 , pp. 123 - 135
Copyright
Copyright © Cambridge Philosophical Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Coven, E. and Meyerowitz, A.Tiling the integers with translates of one finite set. J. Algebra 212 (1999), 161–174.CrossRefGoogle Scholar
[2]Dutkay, D. and Jorgensen, P. On the universal tiling conjecture in dimension one, preprint (2012).CrossRefGoogle Scholar
[3]Farkas, B., Matolcsi, M. and Móra, On Fuglede's conjecture and the existence of universal spectra. J. Fourier Anal. Appl. 12 (2006), 483–494.Google Scholar
[4]Fuglede, B.Commuting self-adjoint partial differential operators and a group theoretic problem. J. Funct. Anal. 16 (1974), 101–121.CrossRefGoogle Scholar
[5]Iosevich, A. and Kolountzakis, M. N. Periodicity of the spectrum in dimension one. http://arxiv.org/abs/1108.5689 (2012).Google Scholar
[6]Kolountzakis, M. N. and Lagarias, J. C.Structure of tiling of the line by a function., Duke Math J. 82 (1996), 653–678.CrossRefGoogle Scholar
[7]Kolountzakis, M. N. and Matolcsi, M. Complex Hadamard matrices and the spectral set conjecture. Collect. Math. Vol Extra (2006), 281–291.Google Scholar
[8]Kolountzakis, M. N. and Matolcsi, M.Tiles with no spectra. Forum Math. 18 (2006), 519–528.CrossRefGoogle Scholar
[9]Łaba, I.The spectral set conjecture and multiplicative properties of roots of polynomials. J. London Math. Soc. 65 (2002), 661–671.CrossRefGoogle Scholar
[10]Lagarias, J. C. and Szabo, S.Universal spectra and tijdemans conjecture on factorization of cyclic groups. J. Four. Anal. Appl. 7 (2001), 63–70.CrossRefGoogle Scholar
[11]Lagarias, J. C. and Wang, Y.Tiling the line with translates of one tile. Inven t. Math. 124 (1996), 341–365.CrossRefGoogle Scholar
[12]Lagarias, J. C. and Wang, Y.Spectral sets and factorizations of finite abelian groups. J. Funct. Anal. 145 (1997), 73–98.CrossRefGoogle Scholar
[13]Matolcsi, M.Fuglede's conjecture fails in dimension 4. Proc. Amer. Math. Soc. 133 (2005), 3021–3026.CrossRefGoogle Scholar
[14]Pedersen, S.Spectral sets whose spectrum is a lattice with a base. J. Funct. Anal. 141 (1996), 496–509.CrossRefGoogle Scholar
[15]Pedersen, S. and Wang, Y.Universal spectra, universal tiling sets and the spectral set conjecture. Math. Scand. 88 (2001), 246–256.CrossRefGoogle Scholar
[16]Szabó, S.A type of factorization of finite abelian groups. Discrete Math. 54 (1985), 121–124.CrossRefGoogle Scholar
[17]Tao, T.Fuglede's conjecture is false in 5 and higher dimensions. Math. Res. Lett. 11 (2004), 251–258.CrossRefGoogle Scholar