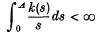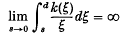Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Atkinson, C.
Reuter, G. E. H.
and
Ridler-Rowe, C. J.
1981.
Traveling Wave Solution for Some Nonlinear Diffusion Equations.
SIAM Journal on Mathematical Analysis,
Vol. 12,
Issue. 6,
p.
880.
Díaz, J. Ildefonso
and
Véron, Laurent
1985.
Local vanishing properties of solutions of elliptic and parabolic quasilinear equations.
Transactions of the American Mathematical Society,
Vol. 290,
Issue. 2,
p.
787.
Bouillet, Julio E.
and
Gomes, Sônia M.
1985.
An equation with a singular nonlinearity related to diffusion problems in one dimension.
Quarterly of Applied Mathematics,
Vol. 42,
Issue. 4,
p.
395.
Duyn, C.J.van
and
Hilhorst, D.
1987.
On a doubly nonlinear diffusion equation in hydrology.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 11,
Issue. 3,
p.
305.
Esteban, Juan R.
and
Vazquez, Juan L.
1988.
Homogeneous diffusion in ? with power-like nonlinear diffusivity.
Archive for Rational Mechanics and Analysis,
Vol. 103,
Issue. 1,
p.
39.
Bernis, F.
1988.
Existence results for doubly nonlinear higher order parabolic equations on unbounded domains.
Mathematische Annalen,
Vol. 279,
Issue. 3,
p.
373.
Wang, Junyu
1990.
A free boundary problem for a generalized diffusion equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 14,
Issue. 8,
p.
691.
Atkinson, C.
1991.
“EXACT” SOLUTION OF A MODEL PROBLEM FOR THE COUPLED THERMOELASTIC EQUATIONS WITH NONSMALL TEMPERATURE CHANGES.
Journal of Thermal Stresses,
Vol. 14,
Issue. 2,
p.
215.
Atkinson, C.
and
Champion, C. R.
1992.
Some boundary-value problems for nonlinear (N) diffusion and pseudo-plastic flow.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 33,
Issue. 3,
p.
255.
Liu, W. B.
and
Barrett, John W.
1993.
Error bounds for the finite element approximation of a degenerate quasilinear parabolic variational inequality.
Advances in Computational Mathematics,
Vol. 1,
Issue. 2,
p.
223.
Liu, W. B.
and
Barrett, John W.
1995.
Quasi-norm error bounds for the finite element approximation of some degenerate quasilinear parabolic equations and variational inequalities.
Numerical Functional Analysis and Optimization,
Vol. 16,
Issue. 9-10,
p.
1309.
Wang, Jun Yu
Gao, Wen Jie
and
Lin, Zheng Hua
1995.
Boundary value problems for general second order equations and similarity solutions to the Rayleigh problem.
Tohoku Mathematical Journal,
Vol. 47,
Issue. 3,
Gilding, B. H.
and
Kersner, R.
1996.
A necessary and sufficient condition for finite speed of propagation in the theory of doubly nonlinear degenerate parabolic equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 126,
Issue. 4,
p.
739.
Lian-Cun, Zheng
Xin-Xin, Zhang
and
Ji-Cheng, He
2004.
Transportation Characteristics for a Class of Generalized
N
-Diffusion Equation with Convection
.
Chinese Physics Letters,
Vol. 21,
Issue. 6,
p.
1104.
Yang, Yu
and
Xiao, Dongmei
2009.
On existence of multiple positive solutions for -Laplacian multipoint boundary value.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 9,
p.
4158.
Staněk, Svatoslav
2009.
Positive solutions of singular Dirichlet boundary value problems with time and space singularities.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 10,
p.
4893.
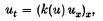
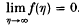 . They show that if k(s) satisfies the condition
. They show that if k(s) satisfies the condition