Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T23:36:06.136Z Has data issue: false hasContentIssue false
  • English
  • Français

Some properties of maximal measures on compact convex sets

Published online by Cambridge University Press:  24 October 2008

C. J. K. Batty
C. J. K. Batty
Affiliation:
Department of Mathematics, University of Edinburgh, Edinburgh EH9 3JZ
Get access Rights & Permissions [Opens in a new window]

Abstract

Let be a maximal measure on a compact convex set K, K* be the state space of the space of all continuous functions f: KK ℝ which are affine in the first variable, 1 be the -algebra on K generated by the Baire sets and the compact extremal subsets of K, and = {B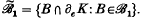eK1}. Then

(i) For any fixed continuous function g:K ℝ and -almost all x in K, there is a closed face of K containing x on which g is constant.

(ii) The image of under the map :KK* defined by f, (x) = f(x, x) is the unique maximal measure on K* representing its barycentre

(iii) induces a measure on (eK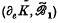) satisfying certain regularity conditions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 2 , September 1983 , pp. 297 - 305
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Alfsen, E. M.Compact convex sets and boundary integrals. (Springer, 1971).CrossRefGoogle Scholar
(2)Abelian, Batty C. J. K.faces of state spaces of C*-algebras. Commun. Math. Phys. 75 (1980), 4350.Google Scholar
(3)Batty, C. J. K. Maximal measures on tensor products of compact convex sets. Quart. J. Math. (Oxford) 33 (1982), 110.Google Scholar
(4)Blackadar, B. E.Traces on simple AF-algebras. J. Funct. Anal. 38 (1980), 156168.CrossRefGoogle Scholar
(5)Bratteli, O., Elliott, G. A. and Kishimoto, A.The temperature state space of a dynamical system I. Yokohama Math. J. 28 (1980), 125167.Google Scholar
(6)Henrichs, R. W.On decomposition theory for unitary representations of locally compact groups. J. Fund. Anal. 31 (1979), 101114.CrossRefGoogle Scholar
(7)Henrichs, R. W.Decomposition of invariant states and non-separable C*-algebras. Publ. Res. Inst. Math. Sci. Kyoto Univ. 18 (1982), 159181.CrossRefGoogle Scholar
(8)Loomis, L. H.Unique direct integral decompositions on convex sets. Amer. J. Math. 84 (1962), 509526.CrossRefGoogle Scholar
(9)Namioka, I. and Phelps, R. R.Tensor products of compact convex sets. Pacific J. Math. 31 (1969), 469480.Google Scholar
(10)Pedersen, G. K.C*-algebras and their automorphism groups (Academic Press, 1979).Google Scholar
(11)Takesaki, M.Theory of operator algebras I (Springer, 1979).Google Scholar
(12)Teleman, S. An introduction to Choquet theory with applications to reduction theory. (Increst preprint, no. 711980.)aGoogle Scholar
(13)Teleman, S. On the regularity of the boundary measures. (Increst preprint, no. 301981.)Google Scholar
(14)Tomita, M.Spectral theory of operator algebras I. Math. J. Okayama Univ. 9 (1959), 6398.Google Scholar
(15)Wils, W.The ideal centre of partially ordered spaces. Acta Math. 127 (1971), 4177.CrossRefGoogle Scholar