Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T14:15:01.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Some metrical theorems in diophantine approximation

v. on a conjecture of mahler

Published online by Cambridge University Press:  24 October 2008

J. W. S. Cassels
J. W. S. Cassels
Affiliation:
The UniversityMachester
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. If ξ is a real number we denote by ∥ ξ ∥ the difference between ξ and the nearest integer, i.e.

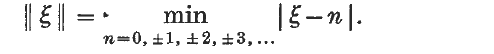
It is well known (e.g. Koksma (3), I, Satz 4) that if θ1, θ2, …, θn are any real numbers, the inequality

has infinitely many integer solutions q > 0. In particular, if α is any real number, the inequality

has infinitely many solutions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 1 , January 1951 , pp. 18 - 21
Copyright
Copyright © Cambridge Philosophical Society 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Khintchine, A.Ya. Zur Theorie der Diophantischen Approximationen. Mat. Sborn. (Rec. Math.), 32 (1925), 277–8.Google Scholar
(2)Khintchine, A.Ya. Zwei Bemerkungen zu einer Arbeit des Herrn Perron. Math. Z. 22 (1925), 274–84.CrossRefGoogle Scholar
(3)Koksma, J. F.Diophantische Approximationen. Ergebn. Math. iv, 4 (1935).Google Scholar
(4)Koksma, J. F.Über die Mahlersche Klasseneinteilung u.s.w. Monatshefte, 48 (1939), 176–89.CrossRefGoogle Scholar
(5)Mahler, K.Über das Mass der Menge aller S-Zahlen. Math. Ann. 166 (1932), 131–9.CrossRefGoogle Scholar
(6) (C.R. Acad. Sci. U.R.S.S.), 67 (1949), 783–6.Google Scholar