Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T14:56:16.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Some James numbers of Stiefel manifolds

Published online by Cambridge University Press:  24 October 2008

Hideaki Ōshima
Hideaki Ōshima
Affiliation:
Osaka City University, Osaka 558, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this note is to determine some unstable James numbers of Stiefel manifolds. We denote the real numbers by R, the complex numbers by C, and the quaternions by H. Let F be one of these fields with the usual norm, and d = dimRF. Let On, k = On, k(F) be the Stiefel manifold of all orthonormal k–frames in Fn, and q: On, k → Sdn−1 the bundle projection which associates with each frame its last vector. Then the James number O{n, k} = OF{n, k} is defined as the index of q* πdn−1(On, k) in πdn−1(Sdn−1). We already know when O{n, k} is 1 (cf. (1), (2), (3), (13), (33)), and also the value of OK{n, k} (cf. (1), (13), (15), (34)). In this note we shall consider the complex and quaternionic cases. For earlier work see (11), (17), (23), (27), (29), (31) and (32). In (27) we defined the stable James number 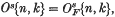, which was a divisor of O{n, k}. Following James we shall use the notations X{n, k}, Xs{n, k}, W{n, k} and Ws{n, k} instead of OH{n, k}, 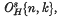, Oc{n, k} and 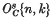respectively. In (27) we noticed that O{n, k} = Os{n, k} if n ≥ 2k– 1, and determined Xs{n, k} for 1 ≤ k ≤ 4, and also Ws{n, k} for 1 ≤ k ≤ 8. On the other hand Sigrist (31) calculated W{n, k} for 1 ≤ k ≤ 4. He informed the author that W{6,4} was not 4 but 8. Since Ws{6,4} = 4 (cf. § 5 below) this yields that the unstable James number does not equal the stable one in general.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 92 , Issue 1 , July 1982 , pp. 139 - 161
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.Vector fields on spheres. Ann. of Math. (2) 75 (1962), 603–632.CrossRefGoogle Scholar
(2)Adams, J. F. and Walker, G.On complex Stiefel manifolds. Proc. Cambridge Phil. Soc. 61 (1965), 81–103.CrossRefGoogle Scholar
(3)Atiyah, M. F. and Todd, J. A.On complex Stiefel manifolds. Proc. Cambridge Phil. Soc. 56 (1960), 342–353.CrossRefGoogle Scholar
(4)Becker, J. C. and Gottlieb, D. H.The transfer map and fibre bundles. Topology 14 (1975), 1–12.CrossRefGoogle Scholar
(5)Bott, R.The space of loops on a Lie group. Michigan Math. J. 5 (1958), 35–61.CrossRefGoogle Scholar
(6)Bott, R.The stable homotopy of the classical groups. Ann. of Math. (2) 69 (1959), 313–337.CrossRefGoogle Scholar
(7)Crabb, M. C. Some James numbers. (Preprint, 1981.)Google Scholar
(8)Furukawa, Y.The homotopy groups πi(SU(3)), πi(SU(4)) and πi(SU(2)) for i = 24, 25, 26 and 27. Bull. Aichi Univ. Ed. Natur. Sci. 27 (1978), 71–79.Google Scholar
(9)Harris, B.On the homotopy groups of the classical groups. Ann. of Math. (2) 74 (1961), 407–413.CrossRefGoogle Scholar
(10)Harris, B.Some calculations of homotopy groups of symmetric spaces. Trans. Amer. Math. Soc. 106 (1963), 174–184.CrossRefGoogle Scholar
(11)Hubbuck, J. R.A note on complex Stiefel manifolds. J. London Math. Soc. (2) 1 (1969), 85–89.CrossRefGoogle Scholar
(12)Imanishi, H.Unstable homotopy groups of classical groups (odd primary components). J. Math. Kyoto Univ. 7 (1967), 221–243.Google Scholar
(13)James, I. M.Cross-sections of Stiefel manifolds. Proc. London Math. Soc. (3) 8 (1958), 536–547.CrossRefGoogle Scholar
(14)James, I. M.The topology of Stiefel manifolds (London Math. Soc. Lecture Notes 24, Cambridge University Press, 1976).Google Scholar
(15)Kervaire, M. A.Some nonstable homotopy groups of Lie groups. Illinois J. Math. 4 (1960), 161–169.CrossRefGoogle Scholar
(16)Knapp, K. Some applications of K–theory to framed bordism: e–invariant and transfer (Habilitationsschrift, Bonn, 1979).Google Scholar
(17)Lundell, A. T.Generalized e–invariants and the numbers of James. Quart. J. Math. Oxford Ser. (2) 25 (1974), 427–440.CrossRefGoogle Scholar
(18)Mimura, M.On the generalized Hopf homomorphism and the higher composition. Part II. πn+i(Sn) for i = 21 and 22. J. Math. Kyoto Univ. 4 –2 (1965), 301–326.Google Scholar
(19)Mimura, M.Quelques groupes d'homotopie metastables des espaces symétriques Sp(n) et U(2n)/Sp(n). C. R. Acad. Sci. Paris 262 (1966), Ser. A, 20–21.Google Scholar
(20)Mimura, M. and Toda, H.The (n + 20)-th homotopy groups of n–spheres. J. Math. Kyoto Univ. 3 – 1 (1963), 37–58.Google Scholar
(21)Mimura, M. and Toda, H.Homotopy groups of SU(3), SE7(4) and Sp(2). J. Math. Kyoto Univ. 3 –2 (1964), 217–250.Google Scholar
(22)Mimura, M. and Toda, H.Homotopy groups of symplectic groups. J. Math. Kyoto Univ. 3 –2 (1964), 251–273.Google Scholar
(23)Mosher, R. E.Some homotopy of stunted complex projective space. Illinois J. Math. 13 (1969), 192–197.CrossRefGoogle Scholar
(24)Oda, N.Some homotopy groups of SU(3), SU(4) and Sp(2). Fukuoka Univ. Sci. Rep. 8 (1978), 77–89.Google Scholar
(25)Oguchi, K.Generators of 2-primary components of homotopy groups of spheres, unitary groups and symplectic groups. J. Fac. Sci. Univ. Tokyo (Sect. IA Math.) 11 (1964/1965), 65–111.Google Scholar
(26)Oguchi, K.Homotopy groups of Sp(n)/Sp(n − 2). J. Fac. Sci. Univ. Tokyo (Sect. IA Math.) 16 (1969/1970), 179–201.Google Scholar
(27)Ōshima, H.On stable James numbers of stunted complex or quaternionic projective spaces. Osaka J. Math. 16 (1979), 479–504.Google Scholar
(28)Ōshima, H.On the homotopy group π2n+9(U(n)) for n ≥ 6. Osaka J. Math. 17 (1980), 495–511.Google Scholar
(29)Rothenberg, M.The J functor and nonstable homotopy groups of the unitary groups. Proc. Amer. Math. Soc. 15 (1964), 264–271.Google Scholar
(30)Serre, J. P.Homologie singulière des espaces fibrés. Ann. of Math. (2) 54 (1951), 425–505.CrossRefGoogle Scholar
(31)Sigrist, F.Groupes d'homotopie des variétés de Stiefel complexes. Comment. Math. Helv. 43 (1968), 121–131.CrossRefGoogle Scholar
(32)Sigrist, F.Sur les nombres de James des variétés de Stiefel complexes. Illinois J. Math. 13 (1969), 198–201.CrossRefGoogle Scholar
(33)Sigrist, F. and Suter, U.Cross-sections of symplectic Stiefel manifolds. Trans. Amer. Math. Soc. 184 (1973), 247–259.CrossRefGoogle Scholar
(34)Steenrod, N. E.The topology of fibre bundles (Princeton University Press, Princeton, 1962).Google Scholar
(35)Toda, H.Composition methods in homotopy groups of spheres (Ann. of Math. Studies 49, Princeton University Press, 1962).Google Scholar
(36)Vastersavendts, M. L. Sur les groupes d'homotopie de SU(n) (Thèse, Université Libre de Bruxelles, 1967).Google Scholar
(37)Walker, G.Estimates for the complex and quaternionic James numbers. Quart. J. Math. Oxford (in the press).Google Scholar