Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T10:24:49.366Z Has data issue: false hasContentIssue false
  • English
  • Français

Some integrals involving Gauss's hypergeometric function and Meijer's G-function

Published online by Cambridge University Press:  24 October 2008

S. D. Bajpai
S. D. Bajpai
Affiliation:
Shri G. S. Technological Institute, Indore, India
Get access Rights & Permissions [Opens in a new window]

Extract

The object of this paper is to evaluate some integrals involving the product of Gauss's hypergeometric function and Meijer's G-function by expressing the G-function as a Mellin–Barnes type integral and interchanging the order of integrations. The integrals are important because on specializing the parameters they lead to many results for MacRobert's E-function, Bessel, Legendre, Whittaker functions and other related functions. In what follows δ is a positive integer and Δ(δ, α) represents the set of parameters

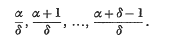
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 4 , October 1967 , pp. 1049 - 1053
Copyright
Copyright © Cambridge Philosophical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Erdélyi, A.Higher transcendental functions, vol. 1 (1953).Google Scholar
(2)Erdélyi, A.Tables of integral transforms, vol. 2 (1954).Google Scholar
(3)MacRobert, T. M.Some integrals involving E-functions. Proc. Glasgow Math. Assoc. 1 (1953), 190–191.CrossRefGoogle Scholar
(4)MacRobert, T. M.Integrals involving hypergeometric functions and E-functions. Proc. Glasgow Math. Assoc. 1 (1958), 196–198.CrossRefGoogle Scholar
(5)MacRobert, T. M.Functions of a complex variable (1962).Google Scholar
(6)Rainville, Earl D.Special functions (1962).Google Scholar
(7)Rathie, C. B.A few infinite integrals involving E-functions. Proc. Glasgow Math. Assoc. 2 (1956), 170–172.CrossRefGoogle Scholar
(8)Saxena, R. K.Some theorems in operational calculus and infinite integrals involving Bessel function and G-functions. Proc. Nat. Inst. Sci. India, Part A 27 (1961), 38–61.Google Scholar
(9)Sharma, K. C.Integrals involving products of G-function and Gauss's hypergeometric function. Proc. Cambridge Philos. Soc. 60 (1964), 539–542.CrossRefGoogle Scholar