Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T18:22:57.857Z Has data issue: false hasContentIssue false
  • English
  • Français

Some generalizations of the Borsuk–Ulam theorem

Published online by Cambridge University Press:  24 October 2008

D. E. Edmunds  and
J. R. L. Webb
D. E. Edmunds
Affiliation:
University of Sussex and University of Glasgow
J. R. L. Webb
Affiliation:
University of Sussex and University of Glasgow
Get access Rights & Permissions [Opens in a new window]

Extract

In a recent paper, Fenn (3) has established the following theorem: if ø is a piecewise linear involution on Sn without fixed points, if f: Sn → Sn and g: 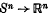are continuous and the degree of f is odd, then there are points x and y on Sn such that f(x) = ø(f(y)) and g(x) = g(y). The Borsuk–Ulam theorem is the special case of this in which f is the identity and ø corresponds to reflexion in the origin. Since an infinite-dimensional version of the Borsuk–Ulam theorem is known, involving compact maps (see, for example, page 72 of (2)), it is natural to ask whether Fenn's result can also be extended to general Banach spaces, and in this paper we give such an extension when ø is reflexion in the origin. More precisely, we prove that if B is the closed unit ball in a Banach space X and f, g: B → X are compact, with deg (I − f, B, 0) odd (this is the Leray–Schauder degree and I is the identity map) and (I − g) (B) contained in a proper, closed subspace of X, then there exist x, y on the boundary ∂B of B and apositive numberα such that α(I − f) (x) = − (I − f) (y) and (I − g) (x) = (I – g) (y).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 1 , July 1977 , pp. 119 - 125
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Amann, H. and Weiss, S.On the uniqueness of the topological degree. Math. Z. 130 (1973), 39–54.CrossRefGoogle Scholar
(2)Deimling, K.Nichtlineare Gleichungen und Abbildungsgrade (Berlin, Heidelberg, New York, Springer-Verlag, 1974).CrossRefGoogle Scholar
(3)Fenn, R.Some generalisations of the Borsuk-Ulam theorem and applications to realizing homotopy classes by embedded spheres. Proc. Cambridge Philos. Soc. 74 (1973), 251–256.CrossRefGoogle Scholar
(4)Joshi, K. D.A non-symmetric generalisation of the Borsuk-Ulam theorem. Fund. Math. 80 (1973), 13–33.CrossRefGoogle Scholar
(5)Joshi, K. D.Infinite dimensional non-symmetric Borsuk-Ulam theorem. Fund. Math. 89 (1975), 45–50.CrossRefGoogle Scholar
(6)Nussbaum, R. D.Degree theory for local condensing maps. J. Math. Anal. Appl. 37 (1972), 741–766.CrossRefGoogle Scholar
(7)Sadovsky, B. N.Limit compact and condensing operators (English translation). Russ. Math. Surveys 27 (1972), 85–155.CrossRefGoogle Scholar
(8)Webb, J. R. L.Remarks on k-set contractions. Boll. U.M.I. (4) 4 (1971), 614–629.Google Scholar
(9)Yosida, K.Functional analysis (Berlin, Göttingen, Heidelberg, Springer-Verlag, 1965).Google Scholar