Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T06:07:37.948Z Has data issue: false hasContentIssue false
  • English
  • Français

Some definite integrals involving Legendre functions

Published online by Cambridge University Press:  24 October 2008

W. N. Bailey
W. N. Bailey
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The integral

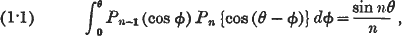
where n is a positive integer, was obtained recently by Van der Pol by operational methods.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 26 , Issue 4 , October 1930 , pp. 475 - 479
Copyright
Copyright © Cambridge Philosophical Society 1930

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Phil. Mag. 8 (1929), 861–898 (70).CrossRefGoogle Scholar

† See G. N. Watson, Theory of Bessel Functions, § 12·2 (4).

‡ G. N. Watson, loc. cit. § 12·2 (3).

§ G. N. Watson, loc. cit. § 12·21.

* G. N. Watson, loc. cit. § 12·2 (4).

† Bailey, W. N., “Some integrals of Kapteyn's type involving Bessel functions”, Proc. London Math. Soc. (2), 30 (1930), 422–424.CrossRefGoogle Scholar See also Bailey, W. N., “Some definite integrals involving Bessel functions”, Proc. London Math. Soc. (2), 31 (1930), 200–208.Google Scholar

* G. N. Watson, loc. cit. § 5·22 (7).