Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-30T20:49:42.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Small independent zeros of quadratic forms

Published online by Cambridge University Press:  24 October 2008

R. J. Cook  and
S. Raghavan
R. J. Cook
Affiliation:
Department of Pure Mathematics, University of Sheffield
S. Raghavan
Affiliation:
Tata Institute for Fundamental Research, Bombay, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let

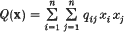
be a non-degenerate quadratic form with integral coefficients. Further, let Q(x) be a zero form, i.e. let there exist x ≠ 0 in ℤn such that Q(x) = 0. Then we know from Cassels[2], (Davenport[6] and ‘a slightly more general result’ from Birch and Davenport [1]) that there exists a ‘small’ solution x in ℤn of the equation Q(x) = 0; more precisely, if

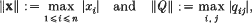
then there exists x ≠ 0 in ℤn such that Q(x) = 0 and further

(Here, and throughout this section, k will denote a number, not necessarily the same at each occurrence, which depends only on n.) An analogue of this estimate for ‘integral’ quadratic forms over algebraic number fields was proved in [8], with the exponent (n − 1)/2 remaining intact.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 1 , July 1987 , pp. 5 - 16
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Birch, B. J. and Davenport, H.. Quadratic equations in several variables. Proc. Cambridge Philos. Soc. 54 (1958), 135–138.CrossRefGoogle Scholar
[2] Cassels, J. W. S.. Bounds for the least solutions of homogeneous quadratic equations. Proc. Cambridge Philos. Soc. 51 (1955), 262–264.CrossRefGoogle Scholar
[3] Cassels, J. W. S.. Addendum to Bounds for…equations. Proc. Cambridge Philos. Soc. 52 (1956), 604.CrossRefGoogle Scholar
[4] Cassels, J. W. S.. Rational quadratic forms (Academic Press, 1978).Google Scholar
[5] Chalk, J. H. H.. Linearly independent zeros of quadratic forms over algebraic number-fields. Monatsh. Math. 90 (1980), 13–25.CrossRefGoogle Scholar
[6] Davenport, H.. Note on a theorem of Cassels. Proc. Cambridge Philos. Soc. 53 (1957), 539–540.CrossRefGoogle Scholar
[7] Davenport, H.. Homogeneous quadratic equations. Mathematika 18 (1971), 1–4.CrossRefGoogle Scholar
[8] Raghavan, S.. Bounds for minimal solutions of diophantine equations. Nachr. Akad. Wiss. Gottingen, Math-Phys. Kl. No. 9 (1975), 109–114.Google Scholar
[9] Schlickewei, H. P.. Kleine Nullstellen homogener quadratischer Gleichungen. Monatsh. Math. 100 (1985), 35–46.CrossRefGoogle Scholar
[10] Schmidt, W. M.. Small zeros of quadratic forms (preprint).Google Scholar
[11] Schulze-Pillot, R.. Small linearly independent zeros of quadratic forms. Monatsh. Math. 95 (1983), 241–249.CrossRefGoogle Scholar
[12] Watson, G. L.. Least solutions of homogeneous quadratic equations. Proc. Cambridge Philos. Soc. 53 (1957), 541–543.CrossRefGoogle Scholar