Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T13:28:49.048Z Has data issue: false hasContentIssue false
  • English
  • Français

S.I.P. measures on metrizable groups

Published online by Cambridge University Press:  24 October 2008

C. Karanikas
C. Karanikas
Affiliation:
University of Crete, Heraclion, Greece
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a metrizable non-discrete locally compact group. Let M(G) be the convolution measure algebra of G. We shall denote by Lx and Rx, x β G, the left and the right translation operation on M(G), respectively. A measure μ β M(G) has strongly independent powers or μ is a s.i.p. measure, if, for x β G and n, m β N,

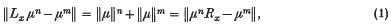
whenever n ≠ m or x ≠ e, where e is the identity of G. If a measure μ satisfies (1) for x = e and n + m, we say that μ has independent powers, or μ is an i.p. measure. Notice that the powers μn and μm of μ are convolution powers.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 3 , May 1983 , pp. 511 - 518
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Brown, G., Karanikas, C. and Williamson, J.The asymmetry of M 0(G). Math. Proc. Cambridge Philos. Soc. 91 (1982), 407–433.CrossRefGoogle Scholar
(2)Dunkl, C. and Ramirez, D.Translations in measure algebras and the correspondence to Fourier transforms vanishing at infinity. Michigan Math. J. 17 (1970), 311–319.CrossRefGoogle Scholar
(3)Graham, C. and Mcgehee, O.Essays in commutative harmonic analysis. Grundlehren der math. Wissenschaften no 238 (Springer-Verlag, 1979).CrossRefGoogle Scholar