Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Sheng-Chi
2014.
Simultaneous nonvanishing of 𝐺𝐿(2)×𝐺𝐿(2) and 𝐺𝐿(2) 𝐿-functions.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 6,
p.
1953.
Liu, Sheng-Chi
2015.
Simultaneous nonvanishing of automorphic L-functions.
Journal of Number Theory,
Vol. 147,
Issue. ,
p.
620.
Blomer, Valentin
and
Milićević, Djordje
2015.
The Second Moment of Twisted Modular L-Functions.
Geometric and Functional Analysis,
Vol. 25,
Issue. 2,
p.
453.
Kıral, Eren
and
Zhou, Fan
2016.
The Voronoi formula and double Dirichlet series.
Algebra & Number Theory,
Vol. 10,
Issue. 10,
p.
2267.
Chen, Guohua
and
Yan, Xiaofei
2018.
Non-vanishing of the first derivative of GL(3) ×GL(2) L-functions.
International Journal of Number Theory,
Vol. 14,
Issue. 03,
p.
847.
Blomer, Valentin
and
Khan, Rizwanur
2019.
Twisted moments of L-functions and spectral reciprocity.
Duke Mathematical Journal,
Vol. 168,
Issue. 6,
Wu, Xiaosheng
2023.
The fourth moment of Dirichlet L-functions at the central value.
Mathematische Annalen,
Vol. 387,
Issue. 3-4,
p.
1199.
Nunes, Ramon M.
2023.
Spectral reciprocity via integral representations.
Algebra & Number Theory,
Vol. 17,
Issue. 8,
p.
1381.
Maiti, Gopal
and
Mallesham, Kummari
2024.
Simultaneous non-vanishing of central values of GL(2)×GL(3) and GL(3) L-functions.
Journal of Number Theory,
Vol. 255,
Issue. ,
p.
62.
Anamby, Pramath
and
Pal, Ritwik
2024.
Determination of a pair of newforms from the product of their twisted central values.
Forum Mathematicum,


 ). In the family of holomorphic newforms
). In the family of holomorphic newforms 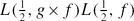 . From this we derive a result on the simultaneous non-vanishing of these
. From this we derive a result on the simultaneous non-vanishing of these 