Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hochberg, Yosef
1976.
A Modification of theT-Method of Multiple Comparisons for a One-Way Layout with Unequal Variances.
Journal of the American Statistical Association,
Vol. 71,
Issue. 353,
p.
200.
Miller, Rupert G.
1977.
Developments in Multiple Comparisons 1966–1976.
Journal of the American Statistical Association,
Vol. 72,
Issue. 360a,
p.
779.


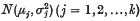 it is possible to construct simultaneous confidence intervals for two given linear functions of population means,
it is possible to construct simultaneous confidence intervals for two given linear functions of population means, 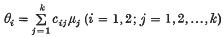 (where
(where 