Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T23:26:32.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Short intervals containing numbers without large prime factors

Published online by Cambridge University Press:  24 October 2008

Glyn Harman
Glyn Harman
Affiliation:
School of Mathematics, University of Wales College of Cardiff, Senghenydd Road, Cardiff CF2 4AG
Get access Rights & Permissions [Opens in a new window]

Extract

We denote, as usual, the number of integers not exceeding x having no prime factors greater than y by Ψ(x, y). We also write

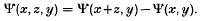
The function Ψ(x, y) is of great interest in number theory and has been studied by many researchers (see [3], [5] and [6] for example). The function Ψ(x, z, y) has also received some attention (see [2], [4–6]). In this paper we shall try to obtain a positive lower bound for Ψ(x, z, y) with y as small as possible when z is about x½ in magnitude. We note that the approach in [5] and [6] allows y to be much smaller than is permissible here, but requires x/z to be smaller than any power of x in [6] (unless some conjecture like the Riemann Hypothesis is assumed), or needs 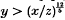in [5]. The following result was obtained by Balog[1].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 1 , January 1991 , pp. 1 - 5
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balog, A.. On the distribution of integers having no large prime factors. Astérisque 147–148 (1987), 27–31.Google Scholar
[2]Balog, A. and Sárközy, A.. On sums of integers having small prime factors: II. Studia Sci. Math. Hungar. 19 (1984), 81–88.Google Scholar
[3]de Bruijn, N. G.. On the number of positive integers ≤ x and free of prime factors ≥ y. Nederl. Akad. Wetensch. Proc. Ser. A 54 (1951), 50–60.CrossRefGoogle Scholar
[4]Friedlander, J. B. and Lagarias, J. C.. On the distribution in short intervals of integers having no large prime factor. J. Number Theory 25 (1987), 249–273.CrossRefGoogle Scholar
[5]Hildebrand, A.. On the number of positive integers ≤ x and free of prime factors ≥ y. J. Number Theory 22 (1986), 289–307.CrossRefGoogle Scholar
[6]Hildebrand, A. and Tenenbaum, G.. On integers free of large prime factors. Trans. Amer. Math. Soc. 296 (1986), 265–290.CrossRefGoogle Scholar
[7]Montgomery, H. L.. Topics in Multiplicative Number Theory (Springer-Verlag, 1971).CrossRefGoogle Scholar
[8]Titchmarsh, E. C.. The Theory of Functions, 2nd ed. (Oxford University Press, 1939).Google Scholar
[9]Titchmarsh, E. C.. The Theory of the Riemann zeta-function, revised by D. R. Heath-Brown (Oxford University Press, 1986).Google Scholar
[10]Walfisz, A.. Weylsche Exponentialsummen in der neueren Zahlentheorie (Deutscher Verlag der Wissenschaften, 1963).Google Scholar