No CrossRef data available.
Shearing transformation of a linear system at an irregular singular point
Published online by Cambridge University Press: 24 October 2008
Extract
Consider an nth-order linear ordinary differential equation

Suppose the αj(x) are holomorphic for x ∈ S, 0 < x0 ≤ |x| < ∞, where S is an open sector of the complex plane with vertex at the origin and positive central angle not exceeding π. Suppose 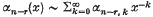 as x → ∞ in each closed subsector of S. The problem of finding a basis for the solutions of (1) can be reduced by a sequence of transformations (see, for example, Gilbert (1)) to the problem of finding a fundamental matrix for a system of the form
as x → ∞ in each closed subsector of S. The problem of finding a basis for the solutions of (1) can be reduced by a sequence of transformations (see, for example, Gilbert (1)) to the problem of finding a fundamental matrix for a system of the form

where q is a non-negative integer, A(x) is an m by m matrix which is holomorphic for x ∈ S, x0 < ≤ |x| < ∞, and 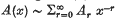 as x → ∞ in each closed subsector of S. If m ≥ 2, A0 is an m by m matrix with elements all zero except for l's on the upper off-diagonal, and the elements of Ar for r ≥ 1 are all zero except possibly in the last row. (There is one such problem (2) for each root, μ of the equation
as x → ∞ in each closed subsector of S. If m ≥ 2, A0 is an m by m matrix with elements all zero except for l's on the upper off-diagonal, and the elements of Ar for r ≥ 1 are all zero except possibly in the last row. (There is one such problem (2) for each root, μ of the equation 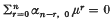 with multiplicity m ≥ 2. Recall that the coefficient αn−r, 0 the first term in the asymptotic expansion of the coefficint αn−r(x) of equation (1).) We denote the elements of the last row of Ar by
with multiplicity m ≥ 2. Recall that the coefficient αn−r, 0 the first term in the asymptotic expansion of the coefficint αn−r(x) of equation (1).) We denote the elements of the last row of Ar by 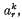 1 ≤ k ≤ m. The system (2) has an irregular singular point at infinity.
1 ≤ k ≤ m. The system (2) has an irregular singular point at infinity.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 1 , January 1981 , pp. 159 - 166
- Copyright
- Copyright © Cambridge Philosophical Society 1981


