Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T12:27:37.287Z Has data issue: false hasContentIssue false
  • English
  • Français

A semigroup embedding problem and an arithmetical function

Published online by Cambridge University Press:  24 October 2008

John M. Howie  and
J. L. Selfridge
John M. Howie
Affiliation:
Department of Mathematical and Computational Sciences, University of St Andrews, North Haugh, St Andrews, Fife, KY16 9SS
J. L. Selfridge
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois, 60115, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

For unexplained terms in semigroup theory see [1] or [4].

Let C, D be classes of semigroups such that every finite semigroup in the class C is embeddable in a finite semigroup in the class D. If n ≥ 2 then k is said to be a C – Dcover of n if every semigroup of order n in the class C is embeddable in a semigroup in the class D of order not greater than k. Let 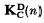be the least C – D cover of n.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 2 , March 1991 , pp. 277 - 286
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Clifford, A. H. and Preston, G. B.. The algebraic theory of semigroups, vol. 1. Math. Surveys no. 7 (American Mathematical Society, 1961).Google Scholar
[2]Giraldes, E.. Semigroups of high rank. II. Doubly noble semigroups. Proc. Edinburgh Math. Soc. (2) 28 (1985), 409–417.CrossRefGoogle Scholar
[3]Giraldes, E. and Howie, John M.. Semigroups of high rank. Proc. Edinburgh Math. Soc. (2) 28 (1985), 13–34.CrossRefGoogle Scholar
[4]Howie, John M.. An Introduction to Semigroup Theory (Academic Press, 1976).Google Scholar
[5]Howie, John M.. Idempotents in completely 0-simple semigroups. Glasgow Math. J. 19 (1978), 109–113.CrossRefGoogle Scholar
[6]Howie, John M.. Embedding semigroups in semibands; some arithmetical results. Quart. J. Math. Oxford Ser. (2) 32 (1981), 323–337.CrossRefGoogle Scholar
[7]Howie, John M.. Arithmetical aspects of semigroup embeddings. In Proceedings Lisbon Conference on Lattices, Semigroups and Universal Algebra. (To appear.)Google Scholar