Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T14:05:07.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Semi-classical bound states of Schrödinger equations

Published online by Cambridge University Press:  21 October 2013

M. SCHECHTER  and
W. ZOU
M. SCHECHTER
Affiliation:
Department of Mathematics, University of California Irvine, CA 92697-3875, U.S.A. e-mail: [email protected]
W. ZOU
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, P.R. China. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the existence of semi-classical bound states of the nonlinear Schrödinger equation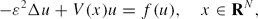

\begin{linenomath}$$ -\varepsilon^2\Delta u+V(x)u=f(u),\quad x\in {\bf R}^N,$$\end{linenomath}
where N ≥ 3;, ϵ is a positive parameter; V:RN → [0, ∞) satisfies some suitable assumptions. We study two cases: if f is asymptotically linear, i.e., if lim|t| → ∞f(t)/t=constant, then we get positive solutions. If f is superlinear and f(u)=|u|p−2u+|u|q−2u, 2* > p > q > 2, we obtain the existence of multiple sign-changing semi-classical bound states with information on the estimates of the energies, the Morse indices and the number of nodal domains. For this purpose, we establish a mountain cliff theorem without the compactness condition and apply a new sign-changing critical point theorem.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 1 , January 2014 , pp. 167 - 181
Copyright
Copyright © Cambridge Philosophical Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ambrosetti, A., Badiale, M. and Cingolani, S.Semiclassical states of nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 140 (1997), 285–300.CrossRefGoogle Scholar
[2]Ambrosetti, A., Malchiodi, A. and Secchi, S.Multiplicity results for some nonlinear Schrödinger equations with potentials. Arch. Ration. Mech. Anal. 159 (2001), 253–271.CrossRefGoogle Scholar
[3]Ambrosotti, A. and Rabinowitz, P. H.Dual variational methods in critical point theory and applications. J. Func. Anal. 14 (1973), 349–381.CrossRefGoogle Scholar
[4]Bartsch, T.Critical point theory on partially ordered Hilbert spaces. J. Funct. Anal. 186 (2001), 117–152.CrossRefGoogle Scholar
[5]Bartsch, T., Liu, Z. and Weth, T.Sign changing solutions of superlinear Schrödinger equations. Comm. Partial Differential Equations 29 (2004), 25–42.CrossRefGoogle Scholar
[6]Brèzis, H. and Lieb, E.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Amer. Math. Soc. 88 (1983), no. 3, 486–490.CrossRefGoogle Scholar
[7]Byeon, J. and Jeanjean, L.Standing waves for nonlinear Schrödinger equations with a general nonlinearity. Arch. Rational Mech. Anal. 185 (2007) 185–200.CrossRefGoogle Scholar
[8]Byeon, J. and Wang, Z. Q.Standing waves with a critical frequency for nonlinear Schrödinger equations II. Calc. Var. Partial Differential Equations 18 (2003), 207–219.CrossRefGoogle Scholar
[9]Conti, M., Merizzi, L. and Terracini, S.Remarks on variational methods and lower-upper solutions. NoDEA 6 (1999), 371–393.CrossRefGoogle Scholar
[10]Conti, M., Merizzi, L. and Terracini, S.On the existence of many solutions for a class of superlinear elliptic systems. J. Differential Equations 167 (2000), 357–387.CrossRefGoogle Scholar
[11]Dancer, N., Lam, K. Y. and Yan, S.The effect of the graph topology on the existence of multipeak solutions for nonlinear Schrödinger equations. Abstr. Appl. Anal. 3 (1998), 293–318.CrossRefGoogle Scholar
[12]Dancer, N. and Yan, S.On the existence of multipeak solutions for nonlinear field equations on $\mathbb{R}^N$. Discrete Contin. Dyn. Syst 6 (2000), 39–50.CrossRefGoogle Scholar
[13]Dávila, J., del Pino, M., Musso, M. and Wei, J.. Standing waves for supercritical nonlinear Schrödinger equations. J. Differential Equations 236 (2007), 164–198.CrossRefGoogle Scholar
[14]Del Pino, M. and Felmer, P. L.. Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differential Equations 4 (1996), 121–137.CrossRefGoogle Scholar
[15]Del Pino, M. and Felmer, P. L.. Semi-classical states for nonlinear Schrödinger equations. J. Funct. Anal. 149 (1997), 245–265.CrossRefGoogle Scholar
[16]Del Pino, M. and Felmer, P. L.. Semi-classical states for nonlinear Schrödinger equations: a variational reduction method. Math. Ann. 324 (2002), 1–32.CrossRefGoogle Scholar
[17]Ding, Y. and Lin, F.Solutions of perturbed Schr?dinger equations with critical nonlinearity. Calc. Var. Partial Differential Equations 30 (2007), 231–249.CrossRefGoogle Scholar
[18]Floer, A. and Weinstein, A.Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69 (1986), 397–408.CrossRefGoogle Scholar
[19]Jeanjean, L. and Tanaka, K.Singularly perturbed elliptic problems with superlinear or asymptotically linear nonlinearities. Calc. Var. Partial Differential Equations 21 (2004), 287–318.CrossRefGoogle Scholar
[20]Kang, X. and Wei, J.On interacting bumps of semi-classical states of nonlinear Schrödinger equations. Adv. Differential Equations 5 (2000), 899–928.CrossRefGoogle Scholar
[21]Jeanjean, L.On the existence of bounded Palais-Smale sequences and application to a Landesman–Lazer type problem set on RN. Proc. Roy. Soc. Edinburgh Sect. A 129 (1999), 787–809.CrossRefGoogle Scholar
[22]Jeanjean, L. Local conditions insuring bifurcation from the continuous spectrum. Math. Z. 232 (1999), 651–664.Google Scholar
[23]Jeanjean, L. Bounded Palais–Smale sequences in minimax theorems and applications to bifurcation theory. Variational problems and related topics (Japanese) (Kyoto, 2000). No. 1181 (2001), 80–86.Google Scholar
[24]Jeanjean, L. and Toland, J. F.Bounded Palais–Smale mountain-pass sequences. C. R. Acad. Sci. Paris Sr. I Math. 327 (1998), 23–28.CrossRefGoogle Scholar
[25]Kavian, O.Introduction à la Théorie des Points Critiques (Springer, New York, 1993).Google Scholar
[26]Li, Y. Y.On a singularly perturbed elliptic equation. Adv. Differential Equations. 2 (1997), 955–980.CrossRefGoogle Scholar
[27]Oh, Y.–G.. Existence of semiclassical bound states of nonlinear Schrödinger equations with potentials of the class (V)a. Comm. Partial Differential Equation 13 (1988), 1499–1519.CrossRefGoogle Scholar
[28]Oh, Y.–G.. Stability of semiclassical bound states of nonlinear Schrödinger equations with potentials. Comm. Math. Phys. 121 (1989), 11–33.CrossRefGoogle Scholar
[29]Rabinowitz, P. H.On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
[30]Rabinowitz, P. H. Multibump solutions of a semilinear elliptic PDE on $\mathbb{R}^n, Degenerate diffusions (Minneapolis, MN, 1991), 175–185, IMA Vol. Math. Appl. 47 (Springer, New York, 1993).Google Scholar
[31]Rozenbljum, G. V.Distribution of the discrete spectrum of singular differential operator. Dokl. Akad. Nauk SSSR 202 (1972), 1012–1015; Soviet Math. Dokl. 13 (1972), 245–249.Google Scholar
[32]Schechter, M.A variation of the mountain pass lemma and applications. J. London Math. Soc. 44 (2) (1991), 491–502.CrossRefGoogle Scholar
[33]Schecher, M. and Zou, W.Sign-changing critical points of linking type theorems. Trans. Amer. Math. Soc. 358 (2006), 5293–5318.CrossRefGoogle Scholar
[34]Solimini, S.A note on compactness-type properties with respect to Lorenz norms of bounded subsets of a Sobolev spaces. Ann. Inst. H. Poincaré-Anal. Non Linéaire 12 (1995), 319–337.CrossRefGoogle Scholar
[35]Strauss, W. A.Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977), 149–162.CrossRefGoogle Scholar
[36]Struwe, M.Variational Methods. Springer, Second Edition, 1996.CrossRefGoogle Scholar
[37]Wang, X.On concentration of positive bound states of nonlinear Schrödinger equations. Comm. Math. Phys. 153 (1993), 229–244.CrossRefGoogle Scholar
[38]Zou, W.Sign-Changing Critical Points Theory (Springer-New York, 2008).Google Scholar
[39]Zou, W. Infinitely many nodal bound states for a Schrödinger equation. preprint.Google Scholar