Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T18:56:59.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Saturated systems of symmetric convex domains; results of Eggleston, Bambah and Woods

Published online by Cambridge University Press:  24 October 2008

Vishwa Chander Dumir  and
Dharam Singh Khassa
Vishwa Chander Dumir
Affiliation:
Centre for Advanced Study in Mathematics, Panjab University, Chandigarh-14.
Dharam Singh Khassa
Affiliation:
Centre for Advanced Study in Mathematics, Panjab University, Chandigarh-14.
Get access Rights & Permissions [Opens in a new window]

Extract

Let K be a closed, bounded, symmetric convex domain with centre at the origin O and gauge function F(x). By a homothetic translate of K with centre a and radius r we mean the set {x: F(x−a) ≤ r}. A family ℳ of homothetic translates of K is called a saturated family or a saturated system if (i) the infimum r of the radii of sets in ℳ is positive and (ii) every homothetic translate of K of radius r intersects some member of ℳ. For a saturated family ℳ of homothetic translates of K, let S denote the point-set union of the interiors of members of ℳ and S(l), the set S ∪ {x: F(x) ≤ l}. The lower density ρℳ(K) of the saturated system ℳ is defined by

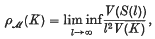
where V(S(l)) denotes the Lebesgue measure of the set S(l). The problem is to find the greatest lower bound ρK of ρℳ(K) over all saturated systems ℳ of homothetic translates of K. In case K is a circle, Fejes Tóth(9) conjectured that

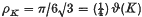
where ϑ(K) denotes the density of the thinnest coverings of the plane by translates of K. In part I, we state results already known in this direction. In part II, we prove that ρK = (¼) ϑ(K) when K is strictly convex and in part III, we prove that ρK = (¼) ϑ(K) for all symmetric convex domains.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 1 , July 1973 , pp. 107 - 116
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bambah, R. P. and Rogers, C. A.Covering the plane with convex sets. J. London Math. Soc. 27 (1952), 304–314.CrossRefGoogle Scholar
(2)Bambah, R. P., Rogers, C. A. and Zassenhaus, H.On coverings with convex domains. Acta Arith. 9 (1964), 191–207.CrossRefGoogle Scholar
(3)Bambah, R. P. and Woods, A. C.On minimal density of the plane coverings by circles. Acta Math. Acad. Sci. Hungar. 19 (3–4) (1968), 337–343.CrossRefGoogle Scholar
(4)Bambah, R. P. and Woods, A. C.On the minimal density of the maximal parkings of the plane by convex bodies. Acta Math. Acad. Sci. Hungar. 19 (1–2), (1968), 103–116.CrossRefGoogle Scholar
(5)Bambah, R. P. and Woods, A. C.The covering constant for a cylinder. Monatah. Math. 72 (1968), 107–117.CrossRefGoogle Scholar
(6)Dumir, Vishwa Chander and Khassa, Dharam SinghA conjecture of Fejes Tóth on saturated systems of circles. Proc. Cambridge Philos. Soc. (To appear.)Google Scholar
(7)Eggleston, H. G.A minimal density plane covering problem. Mathematika 12 (1965), 226–234.CrossRefGoogle Scholar
(8)Eggleston, H. G.Convexity (Cambridge University Press, 1963).Google Scholar
(9)Fejes, Tóth L. Parkings and coverings in the plane. Proc. Coll. Convexity, Copenhagen, 1965 (1967), 78–87.Google Scholar
(10)Sas, E.Über eine Extremumeigenschaft den Ellipsen Compositio. Math. 61 (1939), 468–470.Google Scholar