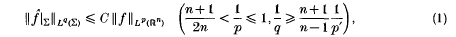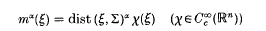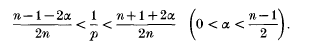Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tao, Terence
1999.
The Bochner-Riesz conjecture implies the restriction conjecture.
Duke Mathematical Journal,
Vol. 96,
Issue. 2,
Tao, Terence
2004.
Fourier Analysis and Convexity.
p.
217.
Mockenhaupt, Gerd
and
Tao, Terence
2004.
Restriction and Kakeya phenomena for finite fields.
Duke Mathematical Journal,
Vol. 121,
Issue. 1,
Lee, Sanghyuk
2005.
Bilinear restriction estimates for surfaces with curvatures of different signs.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 8,
p.
3511.
Rogers, Keith M.
2008.
A local smoothing estimate for the Schrödinger equation.
Advances in Mathematics,
Vol. 219,
Issue. 6,
p.
2105.
Rogers, Keith M.
and
Seeger, Andreas
2010.
Endpoint maximal and smoothing estimates for Schrödinger equations.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 640,
Lee, Sanghyuk
Rogers, Keith M.
and
Seeger, Andreas
2013.
On space–time estimates for the Schrödinger operator.
Journal de Mathématiques Pures et Appliquées,
Vol. 99,
Issue. 1,
p.
62.
Kang, Hunseok
and
Koh, Doowon
2014.
Weak version of restriction estimates for spheres and paraboloids in finite fields.
Journal of Mathematical Analysis and Applications,
Vol. 419,
Issue. 2,
p.
783.
Choi, Yutae
Koh, Youngwoo
and
Lee, Jungjin
2017.
Note on Nikodym maximal in the variable Lebesgue spaces.
Mathematische Nachrichten,
Vol. 290,
Issue. 2-3,
p.
187.
Koh, Doowon
2020.
Conjecture and improved extension theorems for paraboloids in the finite field setting.
Mathematische Zeitschrift,
Vol. 294,
Issue. 1-2,
p.
51.
Gan, Shengwen
Oh, Changkeun
and
Wu, Shukun
2022.
A note on local smoothing estimates for fractional Schrödinger equations.
Journal of Functional Analysis,
Vol. 283,
Issue. 5,
p.
109558.
Wu, Shukun
2023.
On the Bochner-Riesz operator in ℝ3.
Journal d'Analyse Mathématique,
Vol. 149,
Issue. 2,
p.
677.
Hickman, Jonathan
and
Zahl, Joshua
2024.
A note on Fourier restriction and nested Polynomial Wolff axioms.
Journal d'Analyse Mathématique,
Vol. 152,
Issue. 1,
p.
19.
Chen, Xianghong
Guo, Zihua
Shen, Minxing
and
Yan, Lixin
2024.
On smoothing estimates for Schrödinger equations on product spaces Tm×Rn.
Journal of Functional Analysis,
Vol. 286,
Issue. 4,
p.
110262.
Guo, Shaoming
Oh, Changkeun
Wang, Hong
Wu, Shukun
and
Zhang, Ruixiang
2024.
The Bochner–Riesz Problem: An Old Approach Revisited.
Peking Mathematical Journal,
Lu, Yufeng
2024.
Estimates for generalized wave‐type Fourier multipliers on modulation spaces and applications.
Mathematische Nachrichten,
Vol. 297,
Issue. 4,
p.
1468.
Buschenhenke, Stefan
2024.
Factorization in Fourier restriction theory and near extremizers.
Mathematische Nachrichten,
Vol. 297,
Issue. 1,
p.
195.