Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T14:05:43.249Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolving homologies in BPL and PL characteristic numbers

Published online by Cambridge University Press:  24 October 2008

Sandro Buoncristiano  and
Derek Hacon
Sandro Buoncristiano
Affiliation:
University of Naples and Manchester University
Derek Hacon
Affiliation:
University of Naples and Manchester University
Get access Rights & Permissions [Opens in a new window]

Extract

In (1) it was shown that PL characteristic numbers determine (unoriented) PL bordism. In §§ 1 and 2 of this paper we use D. Sullivan's obstruction theory (9), (5) to provide some geometric insight into this result, as follows. We take an unoriented PL manifold M and let νM: M → BPL classify its stable normal bundle, and assume that all its PL characteristic numbers vanish, i.e. that (νM)* [M] = 0, where [M] is the fundamental class of M and 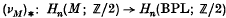. To show that M bounds, we first ‘resolve the homology to zero’ given by (νM)* [M] = 0. This is done by defining obstructions in 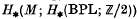whose vanishing ensures that the homology can be ‘resolved’, i.e. can be replaced by a bordism F: W → BPL between νM and a constant map, g: N → BPL, say. Then it is shown that these obstructions all vanish in this case.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 93 , Issue 2 , March 1983 , pp. 263 - 269
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bröcker, T. and Dieck, T. TomKobordismen-theorie. Springer Lecture Notes, no. 178.Google Scholar
(2)Browder, W., Liulevicius, A. and Peterson, F.Cobordism theories. Ann. of Math. 84 (1966), 91–101.Google Scholar
(3)Buoncristiano, S. and Dedò, M.On resolving singularities and relating bordism to homology. Annali S.N.S., Pisa 4 (1980), 605–624.Google Scholar
(4)Buoncristiano, S. and Hacon, D.An elementary geometric proof of two theorems of Thorn. Topology 20 (1981), 97–99.Google Scholar
(5)Kato, M.Topological resolution of singularities. Topology 12 (1973), 355–372.Google Scholar
(6)Kato, M.Partial Poincare duality for k-regular spaces and complex algebraic sets. Topology 16 (1977), 33–50.Google Scholar
(7)Levitt, N. and Rourke, C.Combinatorial formulae for characteristic classes. Trans. Amer. Math. Soc. 239 (1978), 391–397.Google Scholar
(8)Sullivan, D.Combinatorial invariants of analytic spaces. Proc. of Liverpool Singularities Symposium: I. Lecture Notes in Mathematics, no. 209 (1971), 165–168.Google Scholar
(9)Sullivan, D.Singularities in spaces. Proc. of Liverpool Singularities Symposium: II. Lecture Notes in Mathematics, no. 209 (1971), 196–206.Google Scholar