No CrossRef data available.
The resolution of monoidal Cremona transformations of three-dimensional space
Published online by Cambridge University Press: 24 October 2008
Extract
A Cremona transformation Tn, n′ between two three-dimensional spaces is said to be monoidal if the surfaces of order n in one space which form the homaloidal system corresponding to the planes of the second space have a fixed (n − 1)-ple point O. If the surfaces of order n′ forming the homaloidal system in the second space have a fixed (n′ − 1)-ple point O′, the transformation is said to be bimonoidal. A particularly simple bimonoidal transformation is that which transforms lines through O into lines through O′, and planes through O into planes through O′. Such a transformation we shall call an M-transformation. Its equations can, by suitable choice of coordinates, be expressed in the form
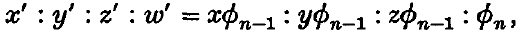
where φn−1(x, y, z, w) = 0, φn(x, y, z, w) = 0 are monoids with vertex (0, 0, 0, 1).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 34 , Issue 1 , January 1938 , pp. 22 - 26
- Copyright
- Copyright © Cambridge Philosophical Society 1938
References
* Pascal, E., Repertorium der höheren Mathematik, ii 2 (Leipzig, 1922), 1032.Google Scholar
† Hudson, H. P., Cremona Transformations (Cambridge, 1927), p. 172.Google Scholar
‡ This transformation is used for the same purpose by Sharpe, F. R. and Snyder, V., “Certain types of involutorial space transformation”, Trans. American Math. Soc. 20 (1919), 185–202CrossRefGoogle Scholar (201).
* Hudson H. P., loc. cit., pp. 306 et seq.
† Montesano, D., “Su le trasformazioni involutorie monoidali”, Rend. Ist. Lombardo (2), 21 (1888), 579–94, 684–7.Google Scholar
‡ Snyder, V., “On the types of monoidal involutions”, Annals of Math. (2), 25 (1924), 279–84.CrossRefGoogle Scholar See also the paper by Sharpe and Snyder previously quoted.


