Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Allenby, R. B. J. T.
and
Tang, C. Y.
1987.
The residual finiteness of a class of 1-relator groups.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 2,
p.
267.
Pride, S. J.
Vernitski, A.
Wong, K. B.
and
Wong, P. C.
2016.
Conjugacy and Other Properties of One-Relator Groups.
Communications in Algebra,
Vol. 44,
Issue. 4,
p.
1588.


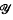 be the class of groups which can be presented in the form
be the class of groups which can be presented in the form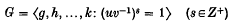
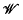 be the class of groups which can be presented in the form
be the class of groups which can be presented in the form