Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-30T19:06:09.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations related to CM elliptic curves

Published online by Cambridge University Press:  24 October 2008

Nigel Boston  and
Stephen V. Ullom
Nigel Boston
Affiliation:
Department of Mathematics, 1409 W. Green Street, University of Illinois, Urbana, IL 61801, U.S.A.
Stephen V. Ullom
Affiliation:
Department of Mathematics, 1409 W. Green Street, University of Illinois, Urbana, IL 61801, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

In [10], Mazur showed that the p-adic lifts of a given absolutely irreducible representation 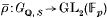are parametrized by a universal deformation ξ:Gℚ, S → GL2(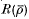) where 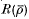has the form 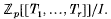. (Here Gℚ, S is the Galois group over ℚ of a maximal algebraic extension unramified outside a finite set S of rational primes.) In [1, 3, 10], situations were investigated where the universal deformation ring turned out to be ℚp[[T1T2, T3]] (i.e. r = 3, I = (0)). In [2], the tame relation of algebraic number theory led to more complicated universal deformation rings, ones whose prime spectra consist essentially of four-dimensional sheets.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 1 , January 1993 , pp. 71 - 85
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Boston, N.. Explicit deformation of Galois representations. Invent. Math. 103 (1991), 181–196.CrossRefGoogle Scholar
[2]Boston, N.. Families of Galois representations – increasing the ramification. Duke Math. J. 66 (1992), 357–367.CrossRefGoogle Scholar
[3]Boston, N. and Mazue, B.. Explicit universal deformations of Galois representations. Adv. Stud. Pure Math. 17 (1989), 1–21.Google Scholar
[4]Bourbaki, N.. Eléments de Mathématique. Algèbre Commutative (Hermann, 1983).Google Scholar
[5]Coates, J. and Flach, M.. Private communication (1988).Google Scholar
[6]Flach, M.. A finiteness theorem for the symmetric square of an elliptic curve. Preprint.Google Scholar
[7]Ireland, K. and Rosen, M.. A Classical Introduction to Modern Number Theory (Springer-Verlag, 1990).CrossRefGoogle Scholar
[8]Jannsen, U. and Wingberg, K.. Die Struktur der absoluten Galoisgruppe p-adischer Zahlkörper. Invent. Math. 70 (1982), 71–98.CrossRefGoogle Scholar
[9]Koch, H.. Galoissche Theorie der p-Erweilerungen (VEB Deutscher Verlag der Wissenschaften, 1970).CrossRefGoogle Scholar
[10]Mazur, B.. Deforming Galois representations. Proceedings of the March 1987 Workshop on “Galois groups of ℚ” held at MSRI, Berkeley, California.Google Scholar
[11]Neukirch, J.. The absolute Galois group of a p-adic number field, Astérisque 94 (1982), 153–164.Google Scholar
[12]Neumann, O.. On p-closed number fields and an analogue of Riemann's existence theorem. In Algebraic Number Fields (Academic Press, 1977), pp. 625–647.Google Scholar
[13]Ribet, K.. Raising the levels of modular representations. Séminaire de Théorie des Nombres, Paris (1987–1988).Google Scholar
[14]Schlessinger, M.. Functors of Artin rings. Trans. Avier. Math. Soc. 130 (1968), 208–222.CrossRefGoogle Scholar
[15]Serre, J.-P.. Propriétés galoisiennes des points d'ordre fini des courbes elliptiques. Invent. Math. 15 (1972), 259–331.CrossRefGoogle Scholar
[16]Serre, J.-P. and Tate, J.. Good reduction of abelian varieties. Ann. of Math. 88 (1968), 492–517.CrossRefGoogle Scholar