Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-16T18:07:33.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on structurally stable proper foliations

Published online by Cambridge University Press:  24 October 2008

Marco Brunella
Marco Brunella
Affiliation:
Dipartimento di Matematica, Piazza di Porta S. Donato 5, I-40127 Bologna, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

Let M be a closed manifold of dimension 3 and let Fol(M) be the space of codimension one C∞-foliations on M. A foliation 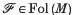∈ Fol(M) is said to be Cr- structurally stable if there exists a neighbourhood V of 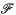in Fol(M) in the (Epstein) Cr-topology such that every foliation 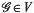is topologically conjugate to 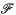, through a homeomorphism near to the identity. Some background on the problem of structural stability of foliations can be found in [8]. In this paper we shall be concerned with proper foliations, i.e. foliations all of whose leaves are proper.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 111 - 120
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bonatti, C.. Sur les feuilletages singuliers stables des variétés de dimension trois. Commun. Math. Helv. 60 (1985), 429–444.CrossRefGoogle Scholar
[2]Cantwell, J. and Conlon, L.. Poincaré-Bendixson theory for leaves of codimension one. Trans. AMS 265 (1981), 181–209.Google Scholar
[3]Dieudonné, J.. Éléments d'analyse, tome I (Gauthier-Villars 1969).Google Scholar
[4]Godbillon, C.. Feuilletages, études géométriques. Birkhauser Progress in Math. 98 (1991).Google Scholar
[5]Goodman, S.. On the structure of foliated 3-manifolds separated by a compact leaf. Inv. Math. 39 (1977), 213–221.CrossRefGoogle Scholar
[6]Hirsch, M.. Stability of compact leaves of foliations, in Dynamical Systems, S. Salvador de Bahia 1971 (ed. Peixoto, ) (Academic Press 1973).Google Scholar
[7]Kopell, N.. Commuting diffeomorphisms. Proc. Symp. Pure Math. XIV (1970), 165–184.CrossRefGoogle Scholar
[8]Rosenberg, H. and Roussabie, R.. Some remarks on stability of foliations. J. Dijf. Geom. 10 (1975), 207–219.Google Scholar
[9]Sternberg, S.. Local C n transformations of the real line. Duke Math. J. 24 (1957), 97–102.CrossRefGoogle Scholar
[10]Yoccoz, J. C.. Centralisateurs et conjugaison différentiables des difféomorphismes du cercle. Thèse d'État, Orsay (1985).Google Scholar