Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T13:16:52.997Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on the K-theory of BГq

Published online by Cambridge University Press:  24 October 2008

Alan Whitley
Alan Whitley
Affiliation:
King's College, London
Get access Rights & Permissions [Opens in a new window]

Extract

1. In (4) Bott and Heitsch discussed certain classifying spaces of importance in the study of foliations of various types. For example they studied the space BГq which helps to classify real foliations of codimension q and proved that a canonical map

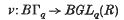
induces an injection in integral cohomology for q ≥ 2. Similar results hold for classifying spaces BUГq and BSГq related to complex and oriented foliations respectively. The object of this paper is to demonstrate that the canonical maps referred to above also induce injections in integral K-theory.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 2 , September 1975 , pp. 309 - 314
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Atiyah, M. F.Characters and cohomology of finite groups. Inst. Hautes Études Sci. Publ. Math. 9 (1961), 23–64.Google Scholar
(2)Atiyah, M. F. and Segal, G.Equivariant K-theory and completion. Differential Geometry 3 (1969), 1–18.Google Scholar
(3)Bott, R.Lecture notes in mathematics 279, Springer-Verlag, New York (1972), 1–94.Google Scholar
(4)Bott, R. and Heitsch, J.A remark on the integral cohomology of BΓq. Topology 11 (1971), 141–146.CrossRefGoogle Scholar
(5)Husemoller, D.Fibre bundles, McGraw-Hill, 1966.Google Scholar
(6)Quillen, D.The spectrum of an equivariant cohomology ring I. Ann. of Math. 94 (1971), 549–572.Google Scholar
(7)Segal, G.The representation ring of a compact Lie group. Inst. Hautes Études Sci. Publ. Math. 34 (1968), 113–128.CrossRefGoogle Scholar
(8)Segal, G.Classifying spaces and spectral sequences. Inst. Hautes Études Sci. Publ. Math. 34 (1968), 105–112.CrossRefGoogle Scholar