Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T21:33:12.554Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Galois module structure of rings of integers and elliptic functions

Published online by Cambridge University Press:  24 October 2008

M. J. Taylor
M. J. Taylor
Affiliation:
Trinity College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let K be a quadratic imaginary number field with discriminant less than −4. For N either a number field or a finite extension of the p-adic field 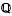p, we let 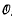N denote the ring of integers of N. Moreover, if N is a number field then we write 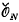for the integral closure of 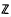[½] in N. For an integral ideal & of 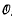K we denote the ray classfield of K with conductor & by K(&). Once and for all we fix a choice of embedding of K into the complex numbers .

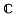Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 3 , November 1983 , pp. 389 - 397
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Abel, N.Oeuvres complètes, ed. Sylow, and Lie, (Christiania, 1881).Google Scholar
(2)Fueter, R.Vorlesungen über die singulären Möduln und die komplexe Multiplikation der elliptischen Funktionen, 1 and 2 (Leipzig-Berlin, 1924).Google Scholar
(3)Hermite, C.Extraits de deux lettres de M. Charles Hermite à M. C.G.J. Jacobi. Crelle 32, 1846.Google Scholar
(4)Martinet, J. Character theory and Artin L-functions. In Algebraic Number Fields (Proc. Durham Symposium), ed. Fröhlich, A. (London, Academic Press, 1977).Google Scholar
(5)Taylor, M. J.Group laws and normal bases. J. reine angew, Math. 337 (1982), 1217–141.Google Scholar
(6)Weber, H.Lehrbuch der Algebra, Bd 3 (Braunschweig, 1908).Google Scholar