Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T14:39:20.382Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity of Hausdorff measure function for conformal dynamical systems

Published online by Cambridge University Press:  17 February 2016

MARIUSZ URBAŃSKI  and
ANNA ZDUNIK
MARIUSZ URBAŃSKI
Affiliation:
Department of Mathematics, University of North Texas, Denton, TX 76203 – 1430, U.S.A. e-mail: [email protected], Web: www.math.unt.edu/~urbanski
ANNA ZDUNIK
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02 – 097 Warszawa, Poland. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We deal with the question of continuity of numerical values of Hausdorff measures in parametrised families of linear (similarity) and conformal dynamical systems by developing the pioneering work of Lars Olsen and the work [SUZ]. We prove Hölder continuity of the function ascribing to a parameter the numerical value of the Hausdorff measure of either the corresponding limit set or the corresponding Julia set. We consider three cases. Firstly, we consider the case of parametrised families of conformal iterated function systems in 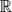$\mathbb{R}$k with k ⩾ 3. Secondly, we consider all linear iterated function systems consisting of similarities in 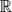$\mathbb{R}$k with k ⩾ 1. In either of these two cases, the strong separation condition is assumed. In the latter case the Hölder exponent obtained is equal to 1/2. Thirdly, we prove such Hölder continuity for analytic families of conformal expanding repellers in the complex plane $\mathbb{C}$. Furthermore, we prove the Hausdorff measure function to be piecewise real–analytic for families of naturally parametrised linear IFSs in 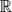$\mathbb{R}$ satisfying the strong separation condition. On the other hand, we also give an example of a family of linear IFSs in 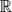$\mathbb{R}$ for which this function is not even differentiable at some parameters.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 3 , May 2016 , pp. 537 - 563
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AS]Ayer, E. and Strichartz, R.Exact Hausdorff measure and intervals of maximum density for Cantor sets. Trans. Amer. Math. Soc. 351 (1999), 3725–3741.Google Scholar
[AU]Akter, H. and Urbański, M.Real analyticity of Hausdorff dimension of Julia sets of parabolic polynomials f λ(z) = z(1 − z − λz 2) Illinois J. Math. 55 (2011), 157–184.Google Scholar
[Bo]Bowen, R.Equilibrium states and the ergodic theory for Anosov diffeomorphisms. Lecture Notes in Math. 470 (Springer, 1975).Google Scholar
[Mi]Mitra, S.Teichmüller spaces and holomorphic motions. J. Anal. Math. 81 (2000), 1–33.Google Scholar
[MSS]Mañé, R.Sad, P. and Sullivan, D.On the dynamics of rational maps. Ann. Sci. École Norm. Sup. (4) 16 (1983), 193–217.CrossRefGoogle Scholar
[Ma]Mattila, P.Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability. Cambridge Stud. Adv. Math. 44 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
[MU]Mauldin, D. and Urbański, M.Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets (Cambridge University Press 2003).CrossRefGoogle Scholar
[OI]Olsen, L.Hausdorff and packing measure functions of self – similar sets: continuity and measurability. Ergodic Theory Dynam. Systems 28 (2008), 1635–1655.Google Scholar
[PU]Przytycki, F. and Urbański, M.Conformal Fractals – Ergodic Theory Methods (Cambridge University Press 2010).Google Scholar
[RU]Roy, M. and Urbański, M.Real analyticity of Hausdorff dimension for higher dimensional hyperbolic graph directed Markov systems. Math. Z. 260 (2008), 153–175.Google Scholar
[Ru1]Ruelle, D.Thermodynamic formalism. Encycl. Math. Appl. vol. 5 (Addison–Wesley, Reading Mass, 1976).Google Scholar
[Ru2]Ruelle, D.Repellers for real analytic maps. Ergodic Theory Dynam. Systems 2 (1982), 99–107.Google Scholar
[SUZ]Szarek, T., Urbański, M. and Zdunik, A.Hausdorff Measure for conformal dynamical systems. Discrete Contin. Dyn. Syst. Series A. 33 (2013), 4647–4692.Google Scholar
[U3]Urbański, M.Analytic families of semihyperbolic generalised polynomial-like mappings. Monatsh. Math. 159 (2010), 133–162.Google Scholar
[UZd]Urbański, M. and Zdunik, A.Real analyticity of Hausdorff dimension of finer Julia sets of exponential family. Ergodic Theory Dynam. Systems 24 (2004), 279–315.CrossRefGoogle Scholar
[UZi]Urbański, M. and Zinsmeister, M.Geometry of hyperbolic Julia–Lavaurs sets. Indag. Math. (N.S.) 12 (2001), 273–292.Google Scholar
[Wa1]Walters, P.An Introduction to Ergodic Theory (Springer-Verlag, 1982).Google Scholar
[Wa2]Walters, P.A variational principle for the pressure of continuous transformations. Amer. J. Math. 97 (1975), 937–971.CrossRefGoogle Scholar
[Zi]Zinsmeister, M.Thermodynamic formalism and holomorphic dynamical systems. SMF/AMS Texts and Monogr. vol.2 (2000).Google Scholar