No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
It has been remarked in a former paper that perhaps a fuller understanding of the theory of linear groups may be arrived at by considering the real representations. It is sufficient that these be irreducible in the real field. In the present paper we continue this investigation and deal with the angles of rotation; in particular we find the form of the commutator
where S and T are substitutions of order p1 and p2 and have angles of rotation θ, θ′, θ″, … and φ, φ′, φ″, …. If certain conclusions regarding the orders of S, T, and C may be drawn we shall then be able to attack a very important problem—;that of Primitivity. This is in essence very similar to the method of Blichfeldt, since the commutator is the product of
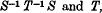
which are both of order p2.
* Proc. Camb. Phil. Soc. 25 (1929), 168–174CrossRefGoogle Scholar. In the middle of page 174 delete: “if they are complex…(to the end of the sentence),” and “This difference…described.”
† Cole, , American Journal of Math. 12 (1890), 191–210.CrossRefGoogle Scholar
* Cf. the important paper by Goursat, , Ann. de l'École Normale, (3) 6 (1889), 9–102CrossRefGoogle Scholar, in which he relates the groups in [4] to the groups on two variables, and thus, by stereographic projection, to the groups of the regular solids in [3], In § 4 we shall compare [4] and [3] directly.
* It is conceivable that the process of stereographic projection might have a further application, i.e. from [2n − 1] to [2n − 2]. This is however not the case. The most general rotation of the hyperephere in [2n − 1] leaves only two points fixed, whereas the fractional substitution
has n fixed points corresponding to the roots of its characteristic equation. These points lie on the quadric
which becomes, when n = 2, the isometric circle in the complex plane. (Cf. Ford, Automorphic Functions, New York, 1929, ch. ii and vi.)