Published online by Cambridge University Press: 24 October 2008
Let 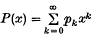 , where pk are complex numbers, have 0 < ρ ≤ ∞ for radius of convergence and assume that P(x) ≠ 0 for α ≤ x < ρ (α < ρ is some real constant). Assuming that
, where pk are complex numbers, have 0 < ρ ≤ ∞ for radius of convergence and assume that P(x) ≠ 0 for α ≤ x < ρ (α < ρ is some real constant). Assuming that 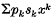 is convergent for all (x ∈ [0, ρ), we define the P-limit of the sequence s = {sk} by
is convergent for all (x ∈ [0, ρ), we define the P-limit of the sequence s = {sk} by
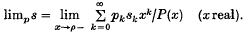
This, so called, power method of limitation (see (3), Definition 9 and (1) Definition 6) will be denoted by P. The best known power methods are Abel's (P(x) = 1/(1 – x), α = 0, ρ = 1) and Borel's (P(x) = ex, α = 0, ρ = ∞). By Cp we denote the set of all sequences, P-limitable to a finite limit and by 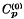 the set of all sequences, P-limitable to zero.
the set of all sequences, P-limitable to zero.