We consider a random walk on a two-dimensional rectangular lattice in which steps are strictly between nearest neighbour points. The conditions of the walk are that the walker must, at each step, turn either to the right or to the left of his previous step with respective probabilities ½(1+α), ½(1−α), (≤ α ≤ 1). To fix the ideas it is assumed that he starts from the origin and the probability of each of the four possible starting directions is ¼. If Ar denotes the probability of return to the origin after r steps we shall show that

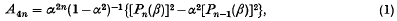
where β = ½(α + α−1) and Pn is the nth Legendre polynomial. It is clear that Ar is zero for r ≢ 0(mod 4).