It is well known that, in the study of quotient spaces it suffices to consider a topological space (X, 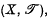), an equivalence relation R on X and the projection mapping p: X → X/R (where X/R is the family of R-classes of X) defined by p(x) = Rx (where Rx is the R-class to which x belongs) for each x ∈ X. A topology 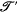may be defined for the set X/R by agreeing that U ⊆ X/R is 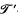-open if and only if p-1 (U) is 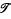-open in X. The topological space 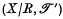is known as the quotient space relative to the space 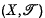) and projection p. If 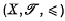(or simply 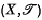) since the symbol ≤ denotes all partial orders and no confusion arises) is a topological ordered space (that is, X is a set for which both a topology 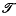and a partial order ≤ is defined) then, providing the projection p satisfies the property

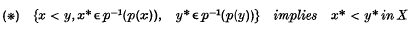
a partial order may be defined in X/R by agreeing that p(x) < p(y) if and only if x < y in x. The topological ordered space 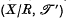is known as the quotient ordered space relative to the ordered space 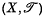and projection p.