No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let V be an infinite-dimensional real Hilbert space with associated C* Clifford algebra C[V]. To any state σ of the C* algebra C[V] there corresponds a skew-adjoint operator C of norm at most unity on V such that
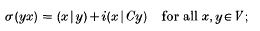
we refer to C as the covariance of the state σ.