Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T13:39:49.171Z Has data issue: false hasContentIssue false
  • English
  • Français

The quarto-quartic transformation of four-dimensional space associated, with certain protectively generated loci

Published online by Cambridge University Press:  24 October 2008

J. A. Todd
J. A. Todd
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The principal object of the present paper is to give a geometrical account of a certain Cremona transformation of four-dimensional space ([4]) into itself. The transformation in question is analogous to the cubo-cubic transformation of [3] which is obtained by drawing cubic surfaces through a twisted sextic curve of genus three, 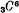. A similar transformation, in space of any number of dimensions, has been described analytically in a note by Godeaux; and most of our work in the present paper extends to the general case. The case of four dimensions is studied here as being less abstract, and more easily susceptible of geometrical treatment; in the general case it is less simple to dispense completely with algebraical methods. We shall see that the various loci which arise in the course of the work are already well known.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 26 , Issue 3 , July 1930 , pp. 323 - 333
Copyright
Copyright © Cambridge Philosophical Society 1930

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See for example Reye, , Geometrie der Lage (5th. ed.), vol. 3, Ch. 18.Google Scholar

† Godeaux, , Rend. Ist. Lomb. (2) 43 (1910) 116.Google Scholar

* Veronese, , Math. Ann. 19 (1882) 215–234.Google Scholar

* Bordiga, , Atti R. Accad. Lincei (Mem.) (4) 4 (1887) 182Google Scholar; White, , Proc. Camb. Phil. Soc. 21 (1922) 216.Google Scholar

* By the usual formula for the residual intersection of surfaces; Salmon, , Geometry of three dimensions (5th ed.), vol. 1, p. 357.Google Scholar

* For the corresponding three-dimensional theory see Hudson, , Cremona Transformations (Cambridge, 1927), pp. 302 seq.Google Scholar

† For applications to the study of quartics through five points see van Kol, , Proc. R. Ac. Sci. Amsterdam, 31 (1928) 620.Google Scholar

* Veneroni, , Rend. Ist. Lomb. (2) 34 (1901) 640.Google Scholar

* White, , Journ. Lond. Math. Soc. 4 (1929) 11.CrossRefGoogle Scholar

* See Wakeford, , Proc. Lond. Math. Soc. (2) 21 (1922) 98.Google Scholar

* Math. Ann. 1 (1869) 413.Google Scholar