Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-30T19:08:35.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Property T for general C*-algebras

Published online by Cambridge University Press:  29 November 2013

CHI–KEUNG NG
CHI–KEUNG NG*
Affiliation:
Chern Institute of Mathematics, Nankai University, Tianjin 300071, China. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we extend the definition of property T and strong property T to general C*-algebras (not necessarily unital). We show that if an inclusion pair of locally compact groups (G,H) has property T, then (C*(G), C*(H)) has property T. As a partial converse, if T is abelian and C*(G) has property T, then T is compact. We also show that if Ω is a first countable locally compact Hausdorff space, then C0(Ω) has (strong) property T if and only if Ω is discrete. Furthermore, the non-unital C*-algebra 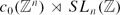$c_0(\mathbb{Z}^n)\rtimes SL_n(\mathbb{Z})$ has strong property T when n ≥ 3. We also give some equivalent forms of strong property T, which are new even in the unital case.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 2 , March 2014 , pp. 229 - 239
Copyright
Copyright © Cambridge Philosophical Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aarne, J. F.On the Mackey-topology for a von Neumann algebra. Math. Scand. 22 (1968), 87–107.Google Scholar
[2]Bekka, M. B.Property (T) for C*-algebras. Bull. London Math. Soc. 38 (2006) 857–867.CrossRefGoogle Scholar
[3]Bekka, M. B., Harpe, P. and Valette, A.Kazhdan's Property (T), (Cambridge University Press, 2008).Google Scholar
[4]Brown, N. P.Kazhdan's property (T) and C*-algebras. J. Funct. Anal. 240 (2006) 290–296.CrossRefGoogle Scholar
[5]Connes, A. and Jones, V.Property T for von Neumann algebras. Bull. Lond. Math. Soc. 17 (1985), 57–62.CrossRefGoogle Scholar
[6]Jolissaint, P.On property (T) for Pairs of topological groups, Enseign. Math. (2) 51 (2005), 31–45.Google Scholar
[7]Kazhdan, D.Connection of the dual space of a group with the structure of its closed subgroups. Funct. Anal. Appl. 1 (1967), 63–65.Google Scholar
[8]Leung, C. W. and Ng, C. K.Property (T) and strong Property (T) for unital C*-algebras. J. Func. Anal. 256 (2009), 3055–3070.CrossRefGoogle Scholar
[9]Leung, C. W., Ng, C. K. and Wong, N. C.Property (T) for non-unital C*-algebras. J. Math. Anal. Appl. 341 (2008), 1102–1106.Google Scholar
[10]Li, D.Property T** for C*-algebras. Acta Math. Sinica. 28 (2012), 1845–1850.Google Scholar
[11]Schaefer, H. H.Topological Vector spaces. GTM 3 (Springer-Verlag, 1971).Google Scholar
[12]Sentilles, F. D. and Taylor, D. C.Factorization in Banach algebras and the general strict topology. Trans. Amer. Math. Soc. 142 (1969), 141–152.Google Scholar
[13]Takesaki, M.Theory of Operator Algebras I (Springer-Verlag, New York, 1979).CrossRefGoogle Scholar
[14]Taylor, D. C.The strict topology for double centralizer algebras. Trans. Amer. Math. Soc. 150 (1970), 633–643.Google Scholar