Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-29T19:46:17.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of certain measures on a topological group

Published online by Cambridge University Press:  24 October 2008

S. W. Drury
S. W. Drury
Affiliation:
University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

We denote by M(G) the space of bounded regular borel measures on a non-discrete locally compact Abelian topological group G. Under the convolution product and norm of total mass M(G) becomes a complex commutative banach algebra. We denote by Φ the space of m.l.f.s (multiplicative linear functionals) on M(G) and by σ the subset of Φ consisting of functionals symmetric in the sense that

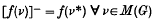
where * denotes the usual involution on M(G). These matters are discussed more fully in Williamson (1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 4 , October 1968 , pp. 1011 - 1013
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Williamson, J. H.Proc. Edinburgh Math. Soc. 11 (1959), 195.CrossRefGoogle Scholar
(2)Williamson, J. H.Proceedings of the Tulane University Symposium on Function Algebras (1965), p. 186; Scott Foresman and Co.Google Scholar
(3)Williamson, J. H.Proceedings of the 5th Matscience Symposium (to appear).Google Scholar
(4)Šreider, Yu. A.Amer. Math. Soc. Transl. 81, Providence 1953.Google Scholar
(5)Gelfand, I. M., Raikov, D. A. and Šilov, G. E.Commutative normed rings. Chelsea.CrossRefGoogle Scholar