Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hernandez, L. J.
and
Porter, T.
1988.
Global analogues of the Brown–Grossman proper homotopy groups of an end.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 104,
Issue. 3,
p.
483.
Ayala, R.
Dominguez, E.
and
Quintero, A.
1989.
Proper homotopy exact sequences for proper fibrations.
Rendiconti del Circolo Matematico di Palermo,
Vol. 38,
Issue. 1,
p.
88.
Ayala, R.
Quintero, A.
and
Dominguez, E.
1990.
A theoretical framework for proper homotopy theory.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 107,
Issue. 3,
p.
475.
Hernández, Luis Javier
and
Porter, Timothy
1992.
An embedding theorem for proper n-types.
Topology and its Applications,
Vol. 48,
Issue. 3,
p.
215.
Hernández, L. J.
and
Porter, T.
1992.
Algebraic Topology Homotopy and Group Cohomology.
Vol. 1509,
Issue. ,
p.
146.
Hernández Paricio, L. J.
1995.
Applications of simplicial 𝑀-sets to proper and strong shape theories.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 2,
p.
363.


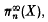 , the Steenrod groups π
, the Steenrod groups π