Proof of the antithetic-variates theorem for unbounded functions
Published online by Cambridge University Press: 24 October 2008
Extract
The method of antithetic variates introduced by Hammersley and Morton (2) is one of the most widely used Monte Carlo techniques for estimating an unknown parameter θ. The basis for this method was established by Hammersley and Mauldon(l).in the case of unbiased estimators with the form
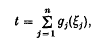
where each of the variates ξj is required to have a uniform marginal distribution over the unit interval [0,1]. By assuming that n = 2 and that the gj are bounded Borel functions, Hammersley and Mauldon showed that the greatest lower bound of var (t) over all admissible joint distributions for the variates ξj can be approached simply by arranging an appropriate strict functional dependence between the ξj. Handscomb(3) extended this result to the case of n > 2 bounded antithetic variates gj(ξj). In many experiments involving distribution sampling or the simulation of some stochastic process over time, the response functions gry are unbounded. This paper further extends the antithetic-variates theorem to include the case of n ≥ 2 unbounded antithetic variates gj(ξj) each with finite variance.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 3 , November 1979 , pp. 477 - 479
- Copyright
- Copyright © Cambridge Philosophical Society 1979
References
REFERENCES
- 14
- Cited by


