Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:47:04.382Z Has data issue: false hasContentIssue false
  • English
  • Français

A proof of Hartman's theorem on compact Hankel operators

Published online by Cambridge University Press:  24 October 2008

F. F. Bonsall  and
S. C. Power
F. F. Bonsall
Affiliation:
University of Edinburgh
S. C. Power
Affiliation:
University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Extract

Let U be a unilateral shift of arbitrary (perhaps uncountable) multiplicity on a Hilbert space. Following Rosenblum (5), an operator A is said to be a Hankel operator relative to U if

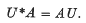
Hartman (2) has characterized the compact Hankel operators relative to the unilateral shift of multiplicity one as the Hankel operators with symbol in H∞ + C(T). Using the usual function space model for representing the unilateral shift, Page ((4), theorem 10) has extended Hartman's theorem to unilateral shifts of countable multiplicity. We give a model-free proof of Hartman's theorem which applies to shifts of arbitrary multiplicity. The proof turns on the observation that a compact operator acts compactly on a certain algebra of operators.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 3 , November 1975 , pp. 447 - 450
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bonsall, F. F. and Rosenthal, P.Certain Jordan operator algebras and double commutant theorems. J. Functional Analysis (to appear).Google Scholar
(2)Hartman, P.On completely continuous Hankel matrices. Proc. Amer. Math. Soc. 9 (1958), 862–866.Google Scholar
(3)Nehari, Z.On bounded bilinear forms. Ann. of Math. 65 (1957), 153–162.Google Scholar
(4)Page, L. B.Bounded and compact vectorial Hankel operators. Trans. Amer. Math. Soc. 150 (1970), 529–539.CrossRefGoogle Scholar
(5)Rosenblum, M. Self-adjoint Toeplitz operators. Summer Institute of Spectral Theory and Statistical Mechanics, 1965, Brookhaven National Laboratory, Upton, New York (1966).Google Scholar
(6)Sz.-Nagy, B. and Foiaş, C.Harmonic analysis of operators on Hilbert space (North Holland, 1970).Google Scholar