Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sunouchi, Gen-Ichirô
1950.
On the strong summability of Fourier series.
Proceedings of the American Mathematical Society,
Vol. 1,
Issue. 4,
p.
526.
Sunouchi, Gen-Ichirô
1951.
On the Walsh-Kaczmarz series.
Proceedings of the American Mathematical Society,
Vol. 2,
Issue. 1,
p.
5.
Tsuchikura, Tamotsu
1956.
Some theorems on Fourier series.
Tohoku Mathematical Journal,
Vol. 8,
Issue. 2,
Sunouchi, Gen-ichirô
1956.
Theorems on power series of the class $H^p$.
Tohoku Mathematical Journal,
Vol. 8,
Issue. 1,
Gosselin, Richard P.
1959.
Some theorems on 𝐿^{𝑝} Fourier series.
Transactions of the American Mathematical Society,
Vol. 92,
Issue. 2,
p.
291.
1964.
A Treatise on Trigonometric Series.
p.
537.
1965.
Multidimensional Singular Integrals and Integral Equations.
p.
241.


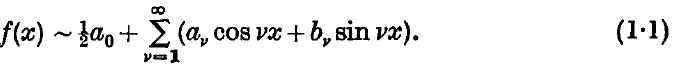
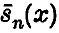 and
and 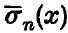 we denote the partial sums and the first arithmetic means of the series
we denote the partial sums and the first arithmetic means of the series
 we mean the function conjugate to
we mean the function conjugate to