Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T13:52:39.332Z Has data issue: false hasContentIssue false
  • English
  • Français

The projective extensions of a finite group

Published online by Cambridge University Press:  24 October 2008

P. J. Webb
P. J. Webb
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a finite group and let g be the augmentation ideal of the integral group ring 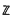G. Following Gruenberg(5) we let (g̱) denote the category whose objects are short exact sequences of zG-modules of the form 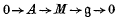and in which the morphisms are commutative diagrams

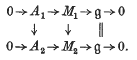
In this paper we describe the projective objects in this category. These are the objects which satisfy the usual categorical definition of projectivity, but they may also be characterized as the short exact sequences

in which P is a projective module.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 251 - 257
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Artamonov, V. A. Private announcement.Google Scholar
(2)Browning, W. Truncated projective resolutions over a finite group, preprint.Google Scholar
(3)Gruenberg, K. W.Cohomological topics in group theory. (Lecture Notes in Math. no. 143, Springer, Berlin, 1970).CrossRefGoogle Scholar
(4)Gruenberg, K. W.Relation modules of finite groups. Amer. Math. Soc. Regional Conf. Ser. 25 (1975).Google Scholar
(5)Gruenberg, K. W. Free abelianised extensions of finite groups, in Homological Group Theory, ed. Wall, C. T. C. (London Math. Soc. Lecture Notes 36, University Press, Cambridge, 1979).Google Scholar
(6)Jacobinski, H.Genera and decomposition of lattices over orders. Acta Math. 121 (1968), 1–29.CrossRefGoogle Scholar
(7)Linnell, P. A.Relation modules and augmentation ideals of finite groups. J. Pure Appl. Algebra (to appear).Google Scholar
(8)McIsaac, A. J. Projectives in some varieties of groups. Thesis (Oxford University, 1976).Google Scholar
(9)Reiner, I.Class groups and Picard groups of group rings and orders. Amer. Math. Soc. Regional Conf. Ser. 26 (1976).Google Scholar
(10)Roggenkamp, K. W. and Hubbr-Dyson, V.Lattices over orders. I (Lecture Notes in Math. no. 115, Springer, Berlin, 1970).CrossRefGoogle Scholar
(11)Roggenkamp, K. W.Lattices over orders. II (Lecture Notes in Math. no. 142, Springer, Berlin, 1970).CrossRefGoogle Scholar
(12)Swan, R. G.Minimal resolutions for finite groups. Topology 4 (1965), 193–208.CrossRefGoogle Scholar
(13)Taylor, M. J.Locally free classgroups of groups of prime power order. J. Algebra 50 (1978), 463–487.CrossRefGoogle Scholar
(14)Webb, P. J.The minimal relation modules of a finite abelian group. J. Pure Appl. Algebra (to appear).Google Scholar
(15)Williams, J. S.Projective objects in categories of group extensions. J. Pure Appl. Algebra 3 (1973), 375–383.CrossRefGoogle Scholar