No CrossRef data available.
Article contents
Projections of the minimal nilpotent orbit in a simple Lie algebra and secant varieties
Published online by Cambridge University Press: 13 July 2023
Abstract
Let G be a simple algebraic group with 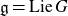 ${\mathfrak g}={\textrm{Lie }} G$ and
${\mathfrak g}={\textrm{Lie }} G$ and 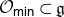 ${\mathcal O}_{\textsf{min}}\subset{\mathfrak g}$ the minimal nilpotent orbit. For a
${\mathcal O}_{\textsf{min}}\subset{\mathfrak g}$ the minimal nilpotent orbit. For a 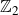 ${\mathbb Z}_2$-grading
${\mathbb Z}_2$-grading 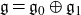 ${\mathfrak g}={\mathfrak g}_0\oplus{\mathfrak g}_1$, let
${\mathfrak g}={\mathfrak g}_0\oplus{\mathfrak g}_1$, let 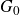 $G_0$ be a connected subgroup of G with
$G_0$ be a connected subgroup of G with 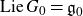 ${\textrm{Lie }} G_0={\mathfrak g}_0$. We study the
${\textrm{Lie }} G_0={\mathfrak g}_0$. We study the 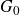 $G_0$-equivariant projections
$G_0$-equivariant projections 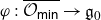 $\varphi\,:\,\overline{{\mathcal O}_{\textsf{min}}}\to {\mathfrak g}_0$ and
$\varphi\,:\,\overline{{\mathcal O}_{\textsf{min}}}\to {\mathfrak g}_0$ and 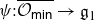 $\psi:\overline{{\mathcal O}_{\textsf{min}}}\to{\mathfrak g}_1$. It is shown that the properties of
$\psi:\overline{{\mathcal O}_{\textsf{min}}}\to{\mathfrak g}_1$. It is shown that the properties of 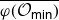 $\overline{\varphi({\mathcal O}_{\textsf{min}})}$ and
$\overline{\varphi({\mathcal O}_{\textsf{min}})}$ and 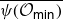 $\overline{\psi({\mathcal O}_{\textsf{min}})}$ essentially depend on whether the intersection
$\overline{\psi({\mathcal O}_{\textsf{min}})}$ essentially depend on whether the intersection 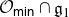 ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1$ is empty or not. If
${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1$ is empty or not. If 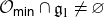 ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1\ne\varnothing$, then both
${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1\ne\varnothing$, then both 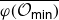 $\overline{\varphi({\mathcal O}_{\textsf{min}})}$ and
$\overline{\varphi({\mathcal O}_{\textsf{min}})}$ and 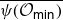 $\overline{\psi({\mathcal O}_{\textsf{min}})}$ contain a 1-parameter family of closed
$\overline{\psi({\mathcal O}_{\textsf{min}})}$ contain a 1-parameter family of closed 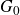 $G_0$-orbits, while if
$G_0$-orbits, while if 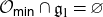 ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1=\varnothing$, then both are
${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1=\varnothing$, then both are 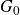 $G_0$-prehomogeneous. We prove that
$G_0$-prehomogeneous. We prove that 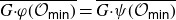 $\overline{G{\cdot}\varphi({\mathcal O}_{\textsf{min}})}=\overline{G{\cdot}\psi({\mathcal O}_{\textsf{min}})}$. Moreover, if
$\overline{G{\cdot}\varphi({\mathcal O}_{\textsf{min}})}=\overline{G{\cdot}\psi({\mathcal O}_{\textsf{min}})}$. Moreover, if 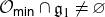 ${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1\ne\varnothing$, then this common variety is the affine cone over the secant variety of
${\mathcal O}_{\textsf{min}}\cap{\mathfrak g}_1\ne\varnothing$, then this common variety is the affine cone over the secant variety of 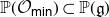 ${\mathbb P}({\mathcal O}_{\textsf{min}})\subset{\mathbb P}({\mathfrak g})$. As a digression, we obtain some invariant-theoretic results on the affine cone over the secant variety of the minimal orbit in an arbitrary simple G-module. In conclusion, we discuss more general projections that are related to either arbitrary reductive subalgebras of
${\mathbb P}({\mathcal O}_{\textsf{min}})\subset{\mathbb P}({\mathfrak g})$. As a digression, we obtain some invariant-theoretic results on the affine cone over the secant variety of the minimal orbit in an arbitrary simple G-module. In conclusion, we discuss more general projections that are related to either arbitrary reductive subalgebras of 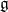 ${\mathfrak g}$ in place of
${\mathfrak g}$ in place of 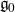 ${\mathfrak g}_0$ or spherical nilpotent G-orbits in place of
${\mathfrak g}_0$ or spherical nilpotent G-orbits in place of 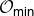 ${\mathcal O}_{\textsf{min}}$.
${\mathcal O}_{\textsf{min}}$.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 3 , November 2023 , pp. 595 - 624
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
Footnotes
This research was funded by RFBR, project no. 20-01-00515.


