Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T13:42:36.736Z Has data issue: false hasContentIssue false
  • English
  • Français

The product of the distributions 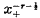and

Published online by Cambridge University Press:  24 October 2008

B. Fisher
B. Fisher
Affiliation:
University of Leicester
Get access Rights & Permissions [Opens in a new window]

Extract

In the following a distribution or a generalized function f is denned, as by Gelfand and Shilov(2) or by Temple (3), as a continuous linear functional on the space K of infinitely differentiable test functions ø having compact support. The value of f at a test function ø will be denoted by (f, ø).

A sequence of test functions {øn} is said to be a null sequence if

(1) the support of each øn is contained in some fixed domain D independent of n,

(2) the sequence 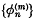converges uniformly to zero in D, as n tends to infinity, for all m.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 1 , January 1972 , pp. 123 - 130
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Fisher, B.The product of distributions. Quart. J. Math. Oxford (2), 22 (1971), 291–8.CrossRefGoogle Scholar
(2)Gelfand, I. M. and Shilov, G. E.Generalized functions, Vol. I (1964).Google Scholar
(3)Temple, G.The theory of generalized functions. Proc. Boy. Soc. Ser. A 28 (1955), 175–190.Google Scholar