Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T23:30:27.059Z Has data issue: false hasContentIssue false
  • English
  • Français

A probabilistic proof of a formula for Jacobi polynomials by L. Carlitz

Published online by Cambridge University Press:  24 October 2008

Paul R. Milch
Paul R. Milch
Affiliation:
Associate Professor, U.S. Naval Postgraduate School
Get access Rights & Permissions [Opens in a new window]

Extract

Let 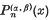be the Jacobi polynomial as defined by Szegö in (7) (see equation (4) below.) Carlitz in (2) presented among others the following formula

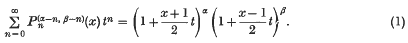
Although, as Carlitz claims, this formula may be derived directly from the definition of Jacobi polynomials, a probabilistic proof such as presented below may shed some new light on formula (1), as well as suggest probabilistic proofs for other similar formulas of Jacobi polynomials, e.g. those given by Manocha and Sharma in (4) and (5) and by Manocha in (3). In addition, it is quite possible that this method of proof will result in the derivation of some new formulas for Jacobi polynomials.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 64 , Issue 3 , July 1968 , pp. 695 - 698
Copyright
Copyright © Cambridge Philosophical Society 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bolshev, L. N.Distributions related to the hypergeometric distribution. Theor. Probability Appl. 4 (1964), 619–624 (English Trans.)CrossRefGoogle Scholar
(2)Carlitz, L.A bilinear generating function for the Jacobi polynomials. Boll. Un. Mat. Ital. 18 (1963).Google Scholar
(3)Manocha, H. L.Some bilinear generating fuuctions for Jacobi polynomials. Proc. Cambridge Philos. Soc. 63 (1967), 457–459.CrossRefGoogle Scholar
(4)Manocha, H. L. and Sharma, B. L.Some formulae for Jacobi polynomials. Proc. Cambridge Philos. Soc. 62 (1967), 459–462.CrossRefGoogle Scholar
(5)Manocha, H. L. and Sharma, B. L.Generating functions of Jacobi polynomials. Proc. Cambridge Philos. Soc. 63 (1967), 431–433.CrossRefGoogle Scholar
(6)Patil, G. P. and Seshadri, V.Characterization theorems for some univariate probability distributions. J. Roy. Statist. Soc. Ser. B 26, 286–292.Google Scholar
(7)Szegö, G.Orthogonal polynomials (New York, 1939).Google Scholar