1. A particle with mass m and coordinates x1x2, x3 relative to a set of rectangular axes fixed in Newtonian space is moving in a field of conservative forces with a potential energy V(x1, x2, x3) and a kinetic energy

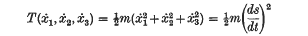
The equations of motion, written

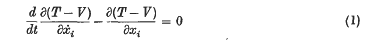
(representing the three equations i = l, i = 2, i = 3 in a way to be used in this paper), constitute, as they stand, a sufficient condition in order to ensure

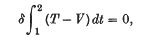
in the sense that the Hamiltonian integral has a stationary value if the actual motion is compared with neighbouring motions with the same terminal positions and the same terminal values of the time as in the actual motion.