Published online by Cambridge University Press: 30 June 2015
The ring A = 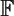 $\mathbb{F}$r[T] and its fraction field k, where r is a power of a prime p, are considered as analogues of the integers and rational numbers respectively. Let K/k be a finite extension and let φ be a Drinfeld A-module over K of rank d and Γ ⊂ K be a finitely generated free A-submodule of K, the A-module structure coming from the action of φ. We consider the problem of determining the number of primes ℘ of K for which the reduction of Γ modulo ℘ is equal to
$\mathbb{F}$r[T] and its fraction field k, where r is a power of a prime p, are considered as analogues of the integers and rational numbers respectively. Let K/k be a finite extension and let φ be a Drinfeld A-module over K of rank d and Γ ⊂ K be a finitely generated free A-submodule of K, the A-module structure coming from the action of φ. We consider the problem of determining the number of primes ℘ of K for which the reduction of Γ modulo ℘ is equal to 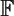 $\mathbb{F}$℘ (the residue field of the prime ℘). We can show that there is a natural density of primes ℘ for which Γ mod ℘ is equal to
$\mathbb{F}$℘ (the residue field of the prime ℘). We can show that there is a natural density of primes ℘ for which Γ mod ℘ is equal to 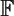 $\mathbb{F}$℘. In certain cases, this density can be seen to be positive.
$\mathbb{F}$℘. In certain cases, this density can be seen to be positive.