Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stroth, Gernot
and
Weiss, Richard
1988.
Geometries and Groups.
p.
513.
Conder, Marston D.E.
and
Walker, Cameron G.
1998.
The Infinitude of 7-Arc-Transitive Graphs.
Journal of Algebra,
Vol. 208,
Issue. 2,
p.
619.
Conder, Marston
2008.
Applications of Group Theory to Combinatorics.
p.
1.
Miklavič, Štefko
Potočnik, Primož
and
Wilson, Steve
2008.
Arc-transitive cycle decompositions of tetravalent graphs.
Journal of Combinatorial Theory, Series B,
Vol. 98,
Issue. 6,
p.
1181.
Conder, Marston
2009.
On symmetries of Cayley graphs and the graphs underlying regular maps.
Journal of Algebra,
Vol. 321,
Issue. 11,
p.
3112.
Potočnik, Primož
2009.
A list of 4-valent 2-arc-transitive graphs and finite faithful amalgams of index (4, 2).
European Journal of Combinatorics,
Vol. 30,
Issue. 5,
p.
1323.
Potočnik, Primož
Spiga, Pablo
and
Verret, Gabriel
2012.
On the nullspace of arc-transitive graphs over finite fields.
Journal of Algebraic Combinatorics,
Vol. 36,
Issue. 3,
p.
389.
Guo, Song-Tao
and
Feng, Yan-Quan
2012.
A note on pentavalent s-transitive graphs.
Discrete Mathematics,
Vol. 312,
Issue. 15,
p.
2214.
Berčič, Katja
and
Ghasemi, Mohsen
2012.
Tetravalent arc-transitive graphs of order twice a product of two primes.
Discrete Mathematics,
Vol. 312,
Issue. 24,
p.
3643.
Morgan, G.L.
2013.
On symmetric and locally finite actions of groups on the quintic tree.
Discrete Mathematics,
Vol. 313,
Issue. 21,
p.
2486.
Potočnik, Primož
2013.
Locally arc-transitive graphs of valence {3,4} with trivial edge kernel.
Journal of Algebraic Combinatorics,
Vol. 38,
Issue. 3,
p.
637.
Guo, Song-Tao
Hua, Xiao-Hui
and
Li, Yan-Tao
2013.
Hexavalent (G, s)-transitive graphs.
Czechoslovak Mathematical Journal,
Vol. 63,
Issue. 4,
p.
923.
Guo, Song-Tao
Hou, Hailong
and
Xu, Yong
2015.
A note on solvable vertex stabilizers of s-transitive graphs of prime valency.
Czechoslovak Mathematical Journal,
Vol. 65,
Issue. 3,
p.
781.
Giudici, Michael
Li, Cai Heng
Seress, Ákos
and
Thomas, Anne
2015.
Characterising vertex-star transitive and edge-star transitive graphs.
Israel Journal of Mathematics,
Vol. 205,
Issue. 1,
p.
35.
Guo, Song-Tao
Feng, Yan-Quan
and
Li, Cai Heng
2015.
Edge-primitive tetravalent graphs.
Journal of Combinatorial Theory, Series B,
Vol. 112,
Issue. ,
p.
124.
Yang, Da-Wei
Feng, Yan-Quan
and
Du, Jia-Li
2016.
Pentavalent symmetric graphs of order2pqr.
Discrete Mathematics,
Vol. 339,
Issue. 2,
p.
522.
Guo, Songtao
Li, Yantao
and
Hua, Xiaohui
2016.
(G,s)-Transitive Graphs of Valency 7.
Algebra Colloquium,
Vol. 23,
Issue. 03,
p.
493.
Du, Jia-Li
Feng, Yan-Quan
and
Zhou, Jin-Xin
2017.
Pentavalent symmetric graphs admitting vertex-transitive non-abelian simple groups.
European Journal of Combinatorics,
Vol. 63,
Issue. ,
p.
134.
Li, Jingjian
Xu, Shangjin
Cao, Mengyue
and
Kang, Zhe
2017.
On tetravalent symmetric dihedrants.
Applied Mathematics and Computation,
Vol. 306,
Issue. ,
p.
49.
Devillers, Alice
Fawcett, Joanna B.
Praeger, Cheryl E.
and
Zhou, Jin-Xin
2020.
On k-connected-homogeneous graphs.
Journal of Combinatorial Theory, Series A,
Vol. 173,
Issue. ,
p.
105234.


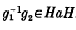 . We will consider this construction only in the case that
. We will consider this construction only in the case that
