Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T02:43:11.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Precompact linear operators in locally convex spaces

Published online by Cambridge University Press:  24 October 2008

J. R. Ringrose
J. R. Ringrose
Affiliation:
St John's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is concerned with the properties of precompact and compact linear operators from a locally convex Hausdorff space 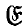into itself, the field of scalars being the complex number field.

The Riesz–Schauder theory for the equations

where T is a compact linear operator from the Bacach space 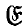into itself, is well known (see, for example, Banach(1), Chapter 10, §2) and has been extended to the more general setting of locally convx Hausdorff spaces by Leray (4). In particular, the ‘Fredholm alternative theorem’ remains valid.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 53 , Issue 3 , July 1957 , pp. 581 - 591
Copyright
Copyright © Cambridge Philosophical Society 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Banach, S.Théorie des operations lineaires (Warsaw, 1932).Google Scholar
(2)Bourbaki, N.Espaces vectoriels topologiques, vols. 1 and 2 (Paris, 1953 and 1955).Google Scholar
(3)Hilbert, D.Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen (Leipzig, 1912).Google Scholar
(4)Leray, J.Acta Sci. Math., Szeged, 12 (1950), 177–86.Google Scholar
(5)Schauder, J.Studia math. 2 (1930), 183–96.CrossRefGoogle Scholar
(6)Williamson, J. H.J. Lond. Math. Soc. 29 (1954), 149–56.CrossRefGoogle Scholar
(7)Altman, M.Studia math. 13 (1953), 194–207.CrossRefGoogle Scholar