Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T19:43:55.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial approximations to the solution of the heat equation

Published online by Cambridge University Press:  24 October 2008

R. E. Scraton
R. E. Scraton
Affiliation:
University of Bradford
Get access Rights & Permissions [Opens in a new window]

Abstract

An approximation is found to the solution of the partial differential equation

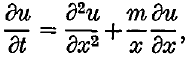
in the region −1 ≤ x ≤ 1, t > 0, where u satisfies a general linear boundary condition on x = ± 1. This approximation is a polynomial in x, and is an exact solution of a perturbed form of the differential equation. By choosing the perturbation appropriately, this approach is mathematically equivalent to some recent methods for solving the differential equation in the form of a Chebyshev series. Better approximations to the required solution (and particularly to the eigenvalues) are obtained by choosing the perturbation to satisfy a least squares criterion.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 73 , Issue 1 , January 1973 , pp. 157 - 165
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Dew, P. M. and Scraton, R. E.An improved method for the solution of the heat equation in Chebyshev series. J. Inst. Math. Appl. 9 (1972), 299.CrossRefGoogle Scholar
(2)Elliott, D.A method for the numerical integration of the one-dimensional heat equation using Chebyshev series. Proc. Cambridge Philos. Soc. 57 (1961), 823.CrossRefGoogle Scholar
(3)Fox, L. and Parker, I. B.Chebyshev Polynomials in Numerical Analysis (Oxford, 1968).Google Scholar
(4)Knibb, D. and Scraton, R. E.On the solution of parabolic partial differential equations in Chebyshev series. Computer J. 14 (1971), 428.CrossRefGoogle Scholar
(5)Lanczos, C.Applied analysis (Prentice-Hall, 1956).Google Scholar
(6)Mason, J. C.A Chebyshev method for the numerical solution of the one-dimensional heat equation. Proc. 22nd ACM Conference (1967), p. 115.Google Scholar