Hostname: page-component-7bb8b95d7b-l4ctd Total loading time: 0 Render date: 2024-09-19T07:10:21.594Z Has data issue: false hasContentIssue false
  • English
  • Français

The Polarisabilities of Atomic Cores

Published online by Cambridge University Press:  24 October 2008

Bertha Swirles
Bertha Swirles
Affiliation:
Yarrow Research Student, Girton College
Get access Rights & Permissions [Opens in a new window]

Extract

If it is assumed that the series electron of an atom polarises the core, then it has been shown by Born and Heisenberg that the polarisability α of the core in a given state may be calculated from the corresponding term value by means of the approximate formulae, 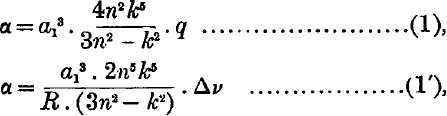where q is the quantum defect, δν is the difference between the term and the corresponding hydrogen term, R is the Rydberg constant in cm.−1, α1 is the radius of first hydrogen orbit, n is the principal quantum number, k is the azimuthal quantum number, For terms with small quantum defect either of the formulae (1) and 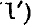may be used, but for terms with large quantum defect (1) gives a higher degree of accuracy.

Type
Articles
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 4 , October 1926 , pp. 403 - 411
Copyright
Copyright © Cambridge Philosophical Society 1926

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Born, M. u. Heisenberg, W., Zeitschr. f. Phys. 23, p. 388, 1924.CrossRefGoogle Scholar

† Schrödinger, E., Ann. d. Phys. (4) 77, p. 43, 1925.CrossRefGoogle Scholar

‡ Kramers, u. Heisenberg, , Zeitschr. f. Phys. 31, p. 681.CrossRefGoogle Scholar

* The term values used were calculated by Mr Hartree from lines given by A. Fowler and the third line of the f-series given by Meiesner; 5g from a probable 4f–5g line given by Paschen-Götze.Google Scholar

‡ The occurrence of two terms with principal quantum number 3 needs some explanation. The unperturbed third orbit, i.e. with term value 12192·8 cm.−1 (see Table 4), has a principal transition frequency 35973·9 cm.−1, which lies very near a resonance frequency of the core. The presence of the core perturbs this orbit and may make it either more or less closely bound; in one case the corresponding transition frequency may be above, in the other below the resonance frequency of the core. If we assume that the smaller transition frequency corresponds to the more closely bound orbit, we can see that both orbits are possible; for an electron in the orbit with smaller transition frequency polarises the core positively so that the orbit is in fact more closely bound, while an electron in the orbit with greater transition frequency polarises the core negatively, so that the core repels it and the orbit is less closely bound. See p. 58 of Schrödinger's paper quoted above.Google Scholar

* Reiche, u. Thomas, , Zeitschr. f. Phys. 34, p. 510.CrossRefGoogle Scholar

† Paschen, , Ann. d. Phys. 71, p. 537.Google Scholar

* All Si terms are taken from a paper by Fowler, A., Phil. Trans. ccxxv, p. 1.Google Scholar

* Millikan, R. A. and Bowen, I. S., Phys. Rev. I. 1. 1924.CrossRefGoogle Scholar